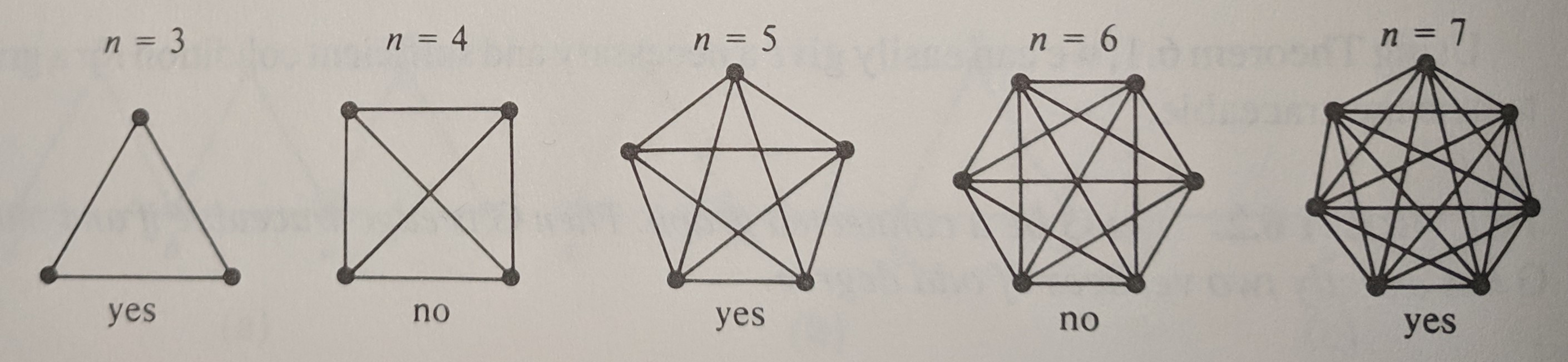Eulerian Graphs
Eulerian graphs are mostly used to solve some practical problems. One major type of problems occur with Eulerian graphs, they are called Traveler's Problems.
An Explorer's problem asks questions like: An explorer wishes to explore all the routes between a number of cities. Can a tour be found which traverses each route only once?
This type of problem focuses on finding a closed trail which includes every edge of the graph. This is actually the definition of a Eulerian graph.
Another way to think of a Eulerian graph is asking whether or not the graph can be drawn without retracing edges or lifting the pencil from the paper (Scaff, 2017)
.
Think back to the section about the beginning of graph theory, and Königsberg bridges problem. This problem asks to find a route crossing each bridge exactly once, this corresponds
exactly to that of finding an Eulerian trail. Thus, the Königsberg bridges problem is an application of Eulerian trails. If you followed the links and tried to solve this puzzle for
yourself, you know that there is no Eulerian trail that exists. A breakdown of Euler's proof of this is presented in
The Truth about Königsberg .
There are other types of problems that are also Eulerian graphs. These other types are Edge-traceable graphs. These are graphs that ask almost the same question as the
Königsberg bridges problem, but instead of ending where you started, this type of problem address whether it is possible to complete this walk by starting and finishing in different
places. One other types is Diagram-Tracing Puzzles, which involve questions about drawing lines to include every square or shape, without crossing into a square of shape twice.
The goal is to do this in as few pen-strokes as possible. For example, the diagram below is easily solved in 4 continuous strokes, but can it be solved in three?
A Eulerian graph is created when the number of points is odd, because they can be drawn in one continuous stroke as shown below.
There are a few other types of problems, which are listed below.Research each of these on your own and try to decide why it is useful to use Eulerian graphs with them.
A ring of Dominions in sequence, Mazes and Labyrinths, and The Chinese Postman Problem.