Georg Cantor made great strides in conceptualizing the actual infinity, and making once very vague and distant ideas more concrete (as concrete as ideas on infinity can be). In reality, there is much more to 'Infinity' than one would originally anticipate. Here, we will discuss the following ideas: cardinality of countably infinite sets, the Hilbert Hotel Paradox, and Cantor's continuum problem.
Countably Infinite Sets
First of all, Cantor made huge strides in being able to define the quantity of elements in an infinite set. There are two specific infinite sets we will focus on: countably infinite sets and uncountably infinite sets. The video podcast above made brief mention to the 'cardinality' of a set. When mathematicians talk about the cardinality of a set, they are referring to the number of elements in a given set. As was mentioned earlier, Cantor determined that the set of Natural numbers was 'actually infinite.' The set of Natural numbers is an example of a countably infinite set: because you can physically 'count' them (1,2,3,4,5,6,...). You never stop counting, but they are countable. Further, he quantified the infinite nature of the cardinality of the set of Natural numbers using the first letter of the Hebrew alphabet: $$\aleph_0$$ This symbol is read "aleph null." Again, this symbol represents the cardinality of the set of Natural numbers.
In set theory, two sets have the same cardinality if you can create a one-to-one correspondence between the elements in those sets; So basically, if you can match up every element in one set with one and only one element in the other set, they have the same cardinality. So, if \(\aleph_0\) is the cardinality of the set of Natural numbers, than any other set we can create a one-to-one correspondence with will have the same cardinality. Take the positive even numbers for example. The Natural numbers (1,2,3,4,5,...) and the even numbers (2,4,6,8,10,...) have the same cardinality because you can create a one-to-one correspondence between the two sets: $$ 1 \rightarrow 2, 2 \rightarrow 4, 3 \rightarrow 6, 4 \rightarrow 8, ...$$ The same kind of one-to-one correspondence could be created between the Natural numbers and the set of all perfect squares (1,4,9,16,25,...): $$ 1 \rightarrow 1, 2 \rightarrow 4, 3 \rightarrow 9, 4 \rightarrow 16, ...$$ At first glance, these examples seem counter-intuitive. Besides, both the set of even numbers and the set of perfect squares are subsets of the Natural numbers! Wouldn't that imply that they have less elements? However, Cantor explained that because of the nature of infinite sets, the cardinality of all these sets really is the same, namely \(\aleph_0\).
Another set that has a cardinality of \(\aleph_0\), that is perhaps even less intuitive, is the set of rational numbers. Consider the graphic to the right taken from Luke Mastin's website on "The Story of Mathematics." Again, we have discussed that in order to conclude that two sets have the same cardinality, we must create a one-to-one correspondence between the two. This image shows how Cantor strategically laid out every rational number in a way that he could create a one-to-one correspondence between that set and the set of Natural numbers. So alas, the set of rational numbers (just like the Natural numbers) is countably infinite!
Now, we typically look at the set of Real numbers as split into two groups: rational and irrational. As we have shown, the set of rational numbers has a cardinality of \(\aleph_0\). We will analyze the cardinality of the set of irrational numbers later on. However, we can also discuss the set of Real numbers being split into two different groups: algebraic numbers and transcendental numbers. Confused yet? Take a look at the picture below to better understand the different sets of numbers we are talking about:

So with a refreshed memory on the different sets of numbers we are dealing with, let's define the set of algebraic numbers. San Jose University defines the set of algebraic numbers as "numbers which are solutions to polynomial equations with integer coefficients." So for example, the equation \(x^2-2=0\) has the solution of \(\sqrt{2}\). Therefore, \(\sqrt{2}\) is an 'algebraic' number. This isn't a special case; take any polynomial equation for example: $$x^2+x-5, x^4-5x^3+3x^2-14, 5x^5+x^3-4x^2+13,...$$ The real solutions, or the real roots, of those polynomial equations are algebraic numbers!
Now, why are we discussing algebraic numbers? Well, we have shown thus far that the Natural numbers, the rational numbers, and other subsets of numbers are COUNTABLY INFINITE. We did this by showing that there is a one-to-one correspondence between the set of Natural numbers and these other sets of numbers. In addition to these sets, the set of algebraic numbers is also countably infinite! Perhaps even less obvious, the set of algebraic numbers are indeed countable, and can be put into a one-to-one correspondence with the Natural numbers. I won't take the time to explain this here, but if you desire a more detailed explanation of the countably infinite nature of the set of algebraic numbers, view this site from San Jose University to see it explained in greater detail.
We could discuss different countably infinite sets for possibly an infinite amount of time! However, what are some of the properties of countably infinite sets? Why do these sets captivate so many mathematicians?
Hilbert's Hotel Paradox
In 1924, a mathematician named David Hilbert came up with the famous paradox known as "Hilbert's Hotel." Never heard of it? Consider watching the following video as an entertaining introduction to this interesting paradox:
For some additional insight into the logic behind this paradox, you may also want to consider the following series of Podcasts:
The basic idea of Hilbert's Hotel is this: Say you have a hotel with infinitely many rooms, and the hotel is filled with infinitely many guests (namely the countable infinity we have been discussing). Well, if a guest showed up desperately needing a room, what would we do? Well, we could have the person in room 1 move to room 2, the person in room 2 move to room 3, the person in room 3 move to room 4, and so on and so on: we would need to have every guest move from room \(n\) to room \(n+1\). How does this make sense? Well, we have discussed how infinity is not an actual number, and that there is not a 'largest' number. So, in the infinite hotel (no matter what room you are in) you can't be in the room with the 'largest' number, so you should be able to move into the room corresponding with the next largest number!
Now, consider the event that an infinitely long bus with infinitely many passengers shows up to your infinity hotel (with seemingly no vacancy) and they all need a room. What do we do?

Well, we have discussed how the set of positive even numbers has the same cardinality as the Natural numbers. So in our hotel, as there are infinitely many rooms, there are also infinitely many even rooms. In order to fit everyone on the infinitely long bus in our hotel, we simply must move the person in room 1 to room 2, the person in room 2 to room 4, the person in room 3 to room 6, the person in room 4 to room 8, and so on and so on. We would need to have every guest move from room \(n\) to room \(2n\). This would leave infinitely many odd numbered rooms for our new guests to occupy.
Why is this helpful? What does this help us understand? Well, in our first encounter with needing to find a room for one extra guest, we just moved every guest to the next room over (or room \(n+1\)). Remembering that the cardinality of a countably infinite set is \(\aleph_0\), this helps illustrate the following idea: $$\aleph_0+1=\aleph_0$$
Further, in our second encounter (with the infinitely long bus) we needed to find a room for infinitely more guests. To accommodate this, we moved everyone from their current room number to the room that was double their current room number; therefore adding infinitely many guests to the hotel that was already booked with infinitely many guests. This helps us illustrate the following: $$ \aleph_0 + \aleph_0 = \aleph_0$$
These are some of the properties of infinity that continue to interest mathematicians today! The fact that adding a countably infinite number of elements to a set that already contains a countably infinite number of elements still gives you a countably infinite set can be mind-blowing! But by definition, it really is the case.
Cantor's Continuum Problem
Note that everything we have done thus far has been in respect to sets that are 'countably infinite.' Sets like the natural numbers and the rational numbers are sets with elements which we can physically count. But how about sets with elements that we can't count, or 'uncountably infinite' sets? Do these sets have a cardinality of \(\aleph_0\), or is it something greater? The following helps us to comprehend the fact that some infinities really are larger than other infinities.
First, let us wrap our minds around the idea of a 'larger' infinity. We have discussed that for a set to be countably infinite, we must be able to form a one-to-one correspondence between that set and the set of Natural numbers. Georg Cantor proved that this CANNOT be done for the entire set of Real numbers in what as known as the diagonal argument. Consider the following image:
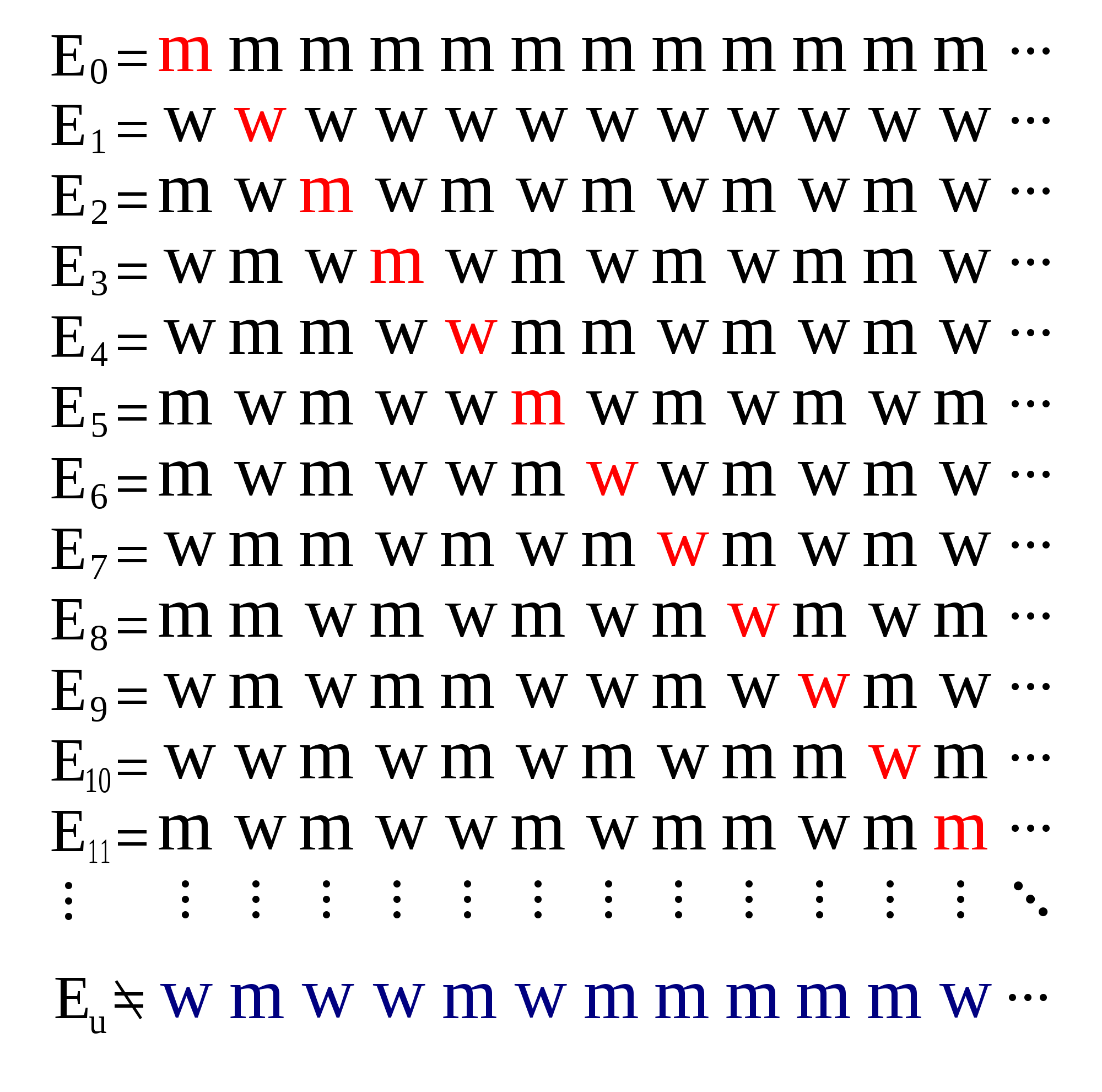
Cantor's diagonal argument follows this basic logic: Consider an infinite set of numbers made up of only two digits (in this case the digits are m's and w's, but they could theoretically be any two digits). The number in blue at the bottom will not be equal to any of the numbers in the set if we ensure that the first digit of the new number is different from the first digit of the first number, the second digit of the new number is different from the second digit of the second number, etc. This argument can be applied to the set of Real numbers, being defined as numbers with a never ending decimal value. Through this argument, Cantor showed that a set with infinitely many elements cannot possible contain all possible real numbers! Therefore, we have introduced an infinity greater than \(\aleph_0\): namely \(\aleph_1\). This \(\aleph_1\) is what Cantor defined as the cardinality of the set of Real numbers
With this, Cantor introduced the idea of the continuum:
So basically, if you take the set of real numbers and split it up such that you have a collection of infinite sets, those sets will have cardinalities of either \(\aleph_0\) or \(\aleph_1\): they will either be countably or uncountably infinite. Cantor also established the following relationship between these two sets: $$2^{\aleph_0}=\aleph_1$$ He also determined that a set with a cardinality in between these two quantities does not exist or in math terms, no set \(S\) exists such that \(\aleph_0<|S|<\aleph_1\).
This is the foundation of Cantor's Continuum Hypothesis. These 'numbers' (\(\aleph_0, \aleph_1, ...\)) are what we call cardinal numbers. They are thus named because they define the quantity of elements in an infinite set (or as we have called it before, the cardinality). Cantor furthered this continuum problem by stating that there are in fact infinitely many cardinal numbers! Namely \(\aleph_0, \aleph_1, \aleph_2, \aleph_3, ..., \aleph_n\).
We really can't physically comprehend the magnitude of infinity, especially as we consider that there are multiple levels of infinity. But at least we can recognize it's important in so much of the mathematics that we do!
