The logistic map is the graphical representation of the recurrence formula above where
xn is a ratio between existing population and maximum population in an environment and r is an adjustable variable that we will evaluate between 0 and 4. This recurrence formula can be understood to mean after an initial x n is determined and x n+1 is computed, that x n+1 value becomes the new x n and is run in the formula again and again for set of solutitons for the equation. With that understanding, engage the below applet.
Using the slider, at what value of r does the behavior become chaotic?
Before the onset point of chaos, the outcomes settles on a single value... then 2... then 4. At about r = 2.57, the maps behavior becomes truely chaotic. The logistic map below actually illustrates the different outcomes of the recurrence relation above.
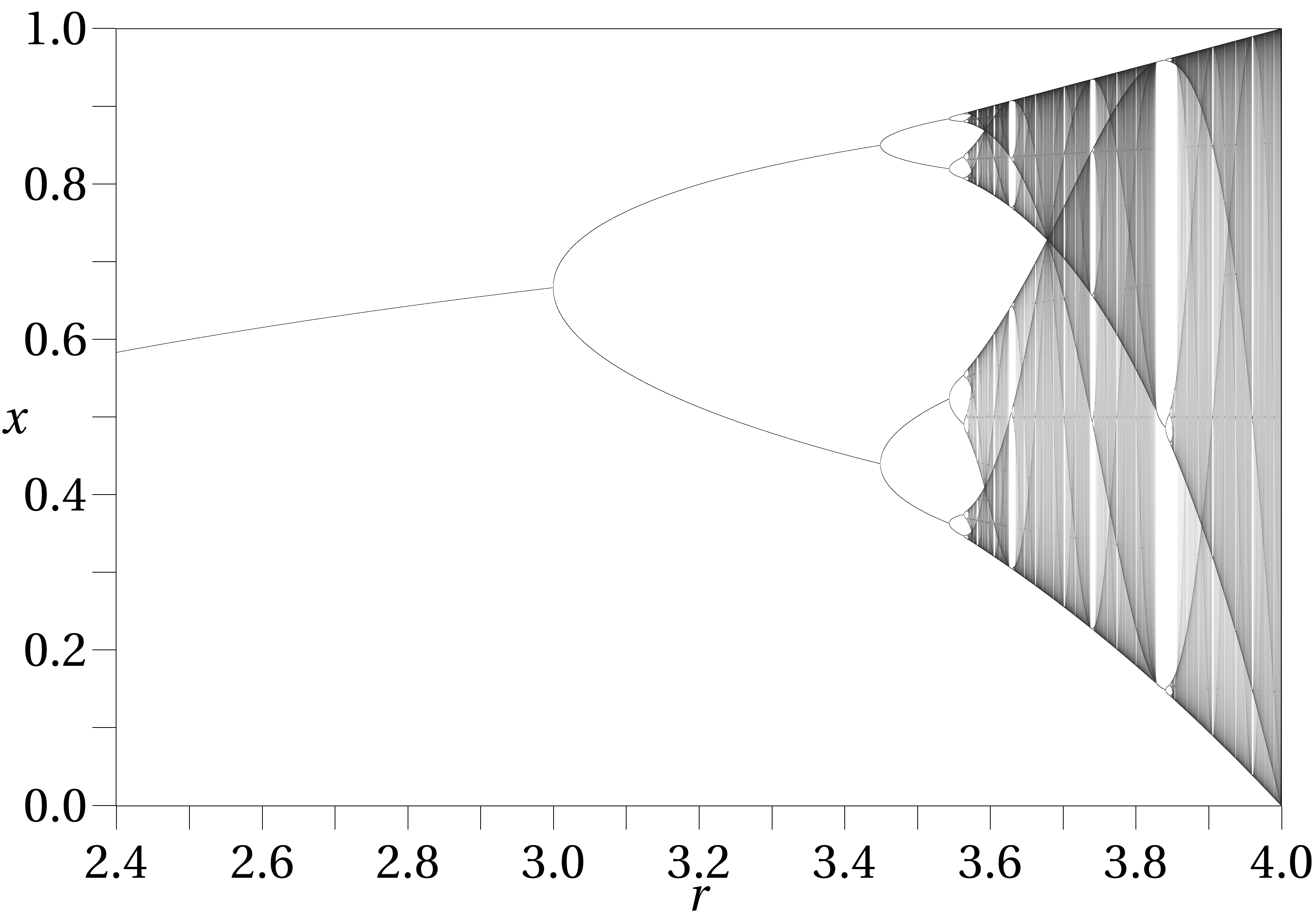
Two interesting observations from the graph are as follows: First, you can also observe periodic periods of relative order in the map. Second, the map is actually self similar- meaning that when you change the scale and zoom into the diagram, you'll observe ever the same behavior as illustrated below.
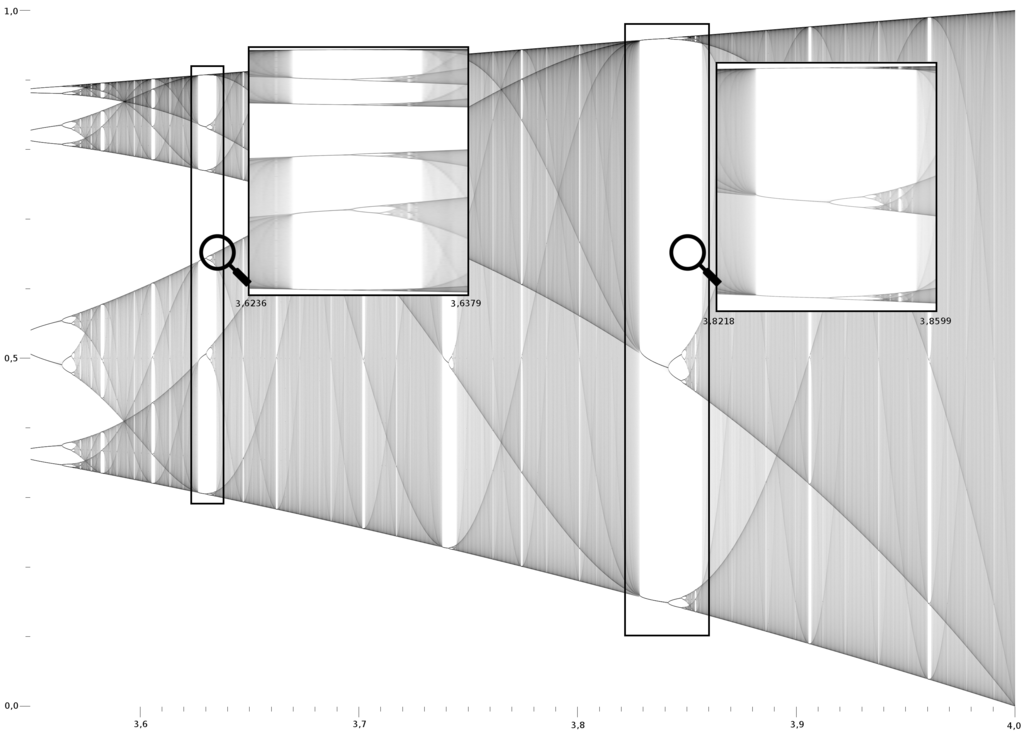
This self similarity is a charicteristic of another mathematical structure observed in nature: the fractal. While this won't be ellaborated upon in depth here, many chaotic systems exibit fractal like behavior and have become a related study for those interested in the world of chaos.
The links below illustrate the relationship between the logistic map and fractals.
Fractal Self Similarity