History and Background


Euclid of Alexandria



(a)

We do not know a lot about Euclid of Alexandria. We have no idea when he was born or when he died. We know from his writings and others that he lived around 300 BCE in the Egyptian city of Alexandria. During Euclid's lifetime Alexandria had just been founded by Alexander the Great (331 BCE). The intention of Alexander was to make Alexandria the intellectual center of the known world. Living here, Euclid would have been surrounded by artists, historians, scholars, philosophers, and mathematicians. In Alexandria he ran his own school and was able to study the works of other philosophers and mathematicians. Many people believe that, "in mathematics all roads lead back to Greece." However, the Greek writers believed otherwise. Aristotle (384-322 BCE) wrote in his Metaphysics, "The Mathematical sciences originated in the neighborhood of Egypt, because there the priestly class was allowed leisure."(1) Proclus, who pays tribute in his Commentary on the First Book of Euclid's Elements, describes the Egyptian understanding of mathematics. "According to most accounts geometry was first discovered among the Egyptians and originated in the measuring of their lands. This was necessary for them because the Nile overflows and obliterates the boundaries between their properties." This was the Hellenistic age that Euclid lived in, a period of time when ideas were shared between civilizations. To the Egyptians, the emphasis of mathematics was primarily utilitarian, yet there were others preceding Euclid that studied math for the sake of finding truth and enlightenment. Within this academic atmosphere Euclid began to organize the knowledge that was available to him in what seemed to be the most logical manner.(2)

(b)
Alexandria Egypt

Influences to Euclid

Euclid is sometimes called the "Father of Geometry." However, he is not the first person to create geometry, as previously stated, nor is he the first mathematician to try to write logical proofs. Having lived just shortly after the Athenian Golden Age, Euclid would have been influenced by Pythagoras, Plato, Aristotle, Hippocrates, and Eudoxus. Many of the mathematical ideas were being used as applied techniques to common ideas believed to be found in nature. Examples of geometry being applied to nature include close estimations of the principles of pi, or the pattern of triples in the Pythagorean principles. Ancient mathematicians used these ideas to make approximations for engineering. They were using inductive methods to look for evidence of unique patterns. To many during this period they believed that mathematics existed and was yet to be discovered. Pythagoras and Plato believed in mathematical realism and believed that naturally occurring objects were waiting to be discovered. Aristotle was more concerned with logic and finding the valid reasoning for how things worked mathematically. Predecessors to Euclid's proof method include Hippocrates, Eudoxus, and Thales. According to Proclus' Commentary on the First Book of Euclid's Elements, "Thales was the first to go into Egypt and bring back this learning [Geometry] into Greece. He discovered many propositions himself and he disclosed to his successors the underlying principles of many others, in some cases his methods being more general, in other more empirical."(3) Thales (624-546 BCE) should be credited with the introduction of logical proof and deductive reasoning rather than intuition and the process of experimenting. So why is Euclid considered the "Father of Geometry" and not Thales? The development of rigorous proof was in its infancy and was being produced during a less known period of Greece philosophy. To understand why Euclid is considered by some more influential you need to look closer at his masterpiece the Elements.


Elements


(c)
Elements Manuscript

Unlike other mathematicians at the time Euclid always offered proofs of his propositions and assigned letters instead of numbers so that he would not be tied to specific values. Using this method he approached mathematics in a more strictly scientific level.(4) It is believed that Euclid wrote over a dozen books, many of which have been lost. Some of his other books include Data, Division of Figures, Phenomena, and Optics. It is known through other sources at the time that two of the lost books included conic sections and logical fallacies. The book Optics investigated theories of vision similar to the philosopher St. Augustine (354-430 AD).(5)) Although each of these book are impressive it is the organization and axiomatic method that Euclid uses in Elements that was so influential. It is astonishing that Elements has survived through the thousands of years. The oldest known edited arrangement of the Elements was compiled by Theon of Alexandria. As far as we knew this was the only known version until an older version was discovered by Francois Peyrard in the Vatican (1808). This manuscript was believed to originate from a Byzantine workshop around 900 CE.(6) The closer proximity to the Middle East allowed the Arabs to receive this transcript around 760 AD and they translated it into Arabic.(7) To the rest of the Western Europe, Elements was lost until 1120 CE when it was translated from Arabic into Latin.(8) This translation would be printed later in 1482 by Erhard Ratdolt of Venice. This book contained not only text but over 400 geometric figures. From this became one of the most widely printed text over the next 500 years, second only to the Bible during this time period. It is from this success and the step-like axiomatic method that it was characterized as the most famous textbook ever published. From this text many philosophers and students during the Scientific Revolution and the Enlightenment period found connection to the classical period of Greek mathematics.(9) It is evident that Elements had a profound influence through history but in the age of discovery some mathematicians and philosophers recognized that there were questions about the logical structure Euclid presented.
A thorough translated online version of all 13 books in Euclid's Elements can be found at this link:
Euclid's Elements Translation .(d) This link also provides commentary on some of the logical criticisms that are presented in the next section. (unfrortunately the javascript has not been updated by the author and his applets are unable to be viewed)


Questions Arise

It is inevitable whenever you state that you have found truth in science there will be others that review and critically analyze the findings. With new understanding of science some scholars tried to find fault in Euclid's proofs and figures. However, if you look at the structure of Elements it invites the reader to analyze, correct, and even simplify Euclid's process. Many of the questions of logic are directed to the first book.(10) The famous British logician Bertrand Russell (1872-1970) once said, "In the beginning everything is self-evident, and it is hard to see whether one self-evident proposition follows from another or not. Obviousness is always the enemy of correctness."(11) The very first proposition asks the reader to create two circles from center points A and B with the radius AB. This as a result creates two intersection points of the overlapping circles. However, there was never a postulate or proof that circles could intersect. Other criticism came from the use of superposition or moving objects on top of each other to prove that figures are congruent.(12)

The most significant and influential criticisms is directed at the Fifth Postulate. The first four are straightforward and relatively easy to understand. However, there is something strange about the Fifth Postulate. It is not as direct and it is would not be considered self-evident. It seems as though Euclid was stumbling over his words. Some scholars have even suggested that Euclid was not quite convinced of the accuracy of the postulate. "From antiquity, there had been discomfort with this fifth postulate, an odd man out among the postulates. The obvious remedy was to find a way to deduce the fifth postulate from the other four. If that could be done, then the fifth postulate would become a theorem and the awkwardness of needing to postulate it would evaporate."(13) Many scholars turned their back on Euclid's Elements believing that it no longer could stand up to a more rigorous logical proof. Others worked exhaustively to try and find proof that the fifth postulate was logically sound. In this effort an indirect strategy was formed to proceed with the first four postulates and negate the fifth. The results continued to come back that there was a necessity for the Fifth Postulate or plainer geometry would contradict the first four postulates. Eventually, mathematicians like Gauss, Riemann, Bolyai, and Lobachevsky recognized that it was not a failure but an alternative geometry. Without assuming the parallel conditions of lines it opened the door to non-Euclidean geometry that was not restricted to the plainer Euclidean space.(14) This discovery was significant in the frontiers of mathematics however Euclid's Elements would influence many others.
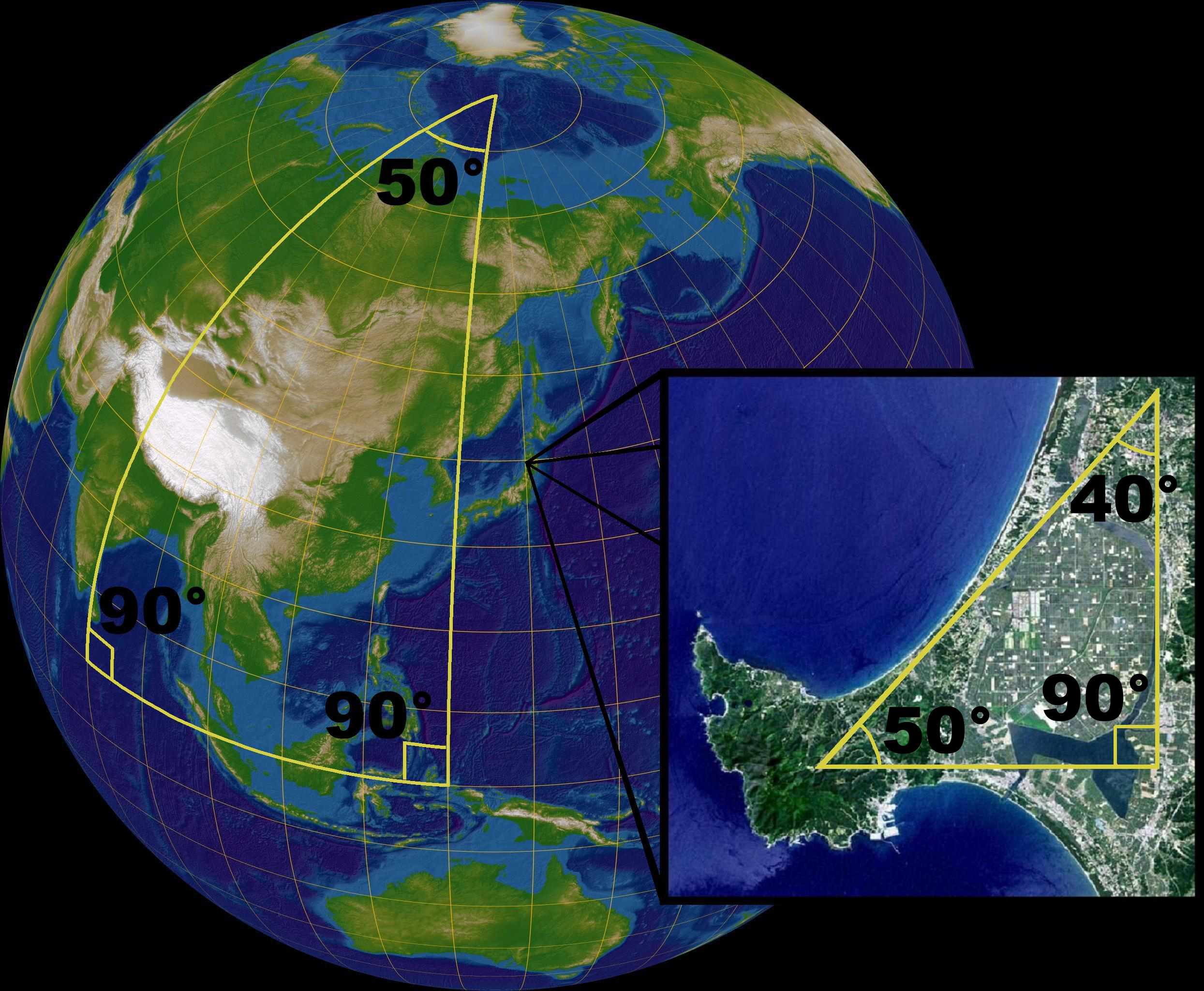(e)


Section Description
History and Background This section of the wepage introduces Euclid, who influenced him, Elements, and questions that arise from Elements.
Significance and Application This section addresses the influnce of Elements and applications into other fields of study.
Explanation of Mathematics This section looks at how Elements is organized, explains inductive and deductive principles, and provides a few examples of proofs
References This section provides the references cited in this webpage.


Top
Main page