To find the volume of a rectangular prism we multiply the values for the length(l) width(w) and height(h) together. This results in the formula lwh= volume (rectangular prism).
Volume of Right Prisms
A right prism is a prism with flat surfaces that has two bases that are congruent polygons and all of the lateral sides are rectangles. The rectangular prism discussed above is a simple example of a right prism that has rectangles for the bases. The volume of any right prism can be discussed in the terms of the height and the area of the base.
We can find this formula using the formula for the volume rectangular prism, area=lwh.All of the heights, h, of the lateral sides of a rectangular prism are equal, and if we substitute for (lw) in the formula for the volume of a rectangular prism with B (area of the base) we find that the volume of a rectangular prism is the product of the area of the base and the height, volume=Bh.
This formula can be used for any volume of any right prism, so long as the appropriate formula for the area of the base is used.
Surface Area of a Rectangular Prism
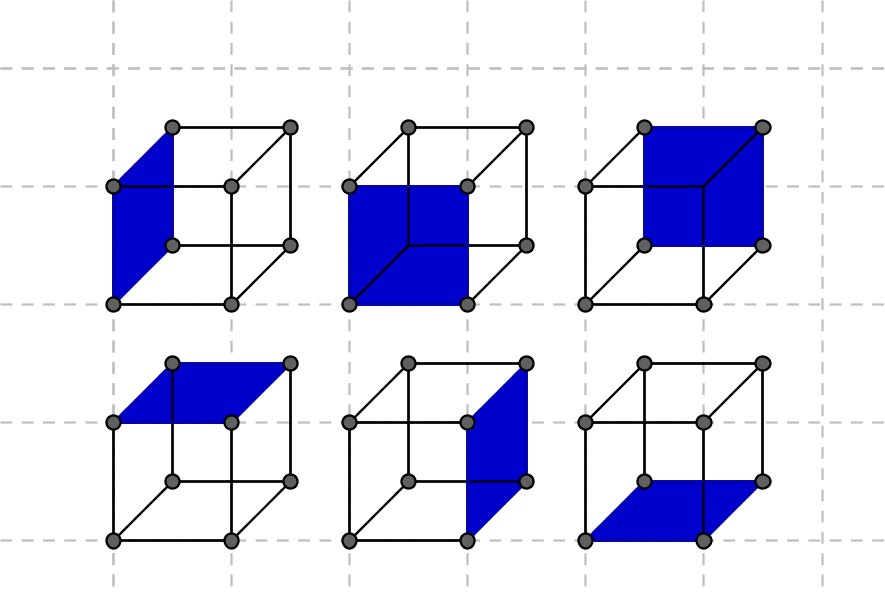The Surface Area of a rectangular prism is the sum of the areas of each individual side.
The area of each of the six sides of the rectangular prism has two of the dimensions of the prism: length, width and height. If we add the areas of each of the sides together we find:
lw+lw+lh+lh+hw+hw = 2lw+2lh+2hw = 2(lw+lh+lw)= SA(rectangular prism).
Surface Area of Right Prisms
To find the surface area of a right prism we sum the areas of all the sides. Right prisms have two congruent polygons for bases, so the sum of the areas of these two bases is 2B. Each of the lateral sides of the prism have the same height, but have the width of one of the sides of the bases.
If the base has n sides the area of any given side is hsi where si is any given one of the sides of the base. The formula for the surface area of a right prism is 2B+(hs1+hs2+hs3...+...hsi+...+hsn). We
can simplify this into a more simple form by factoring h out of the second part of the formula, such that 2B+h(s1+s2+s3...+...si+...+sn). Notice that (s1+s2+s3...+...si+...+sn)
is the sum of all of the sides of the base. Which means that s1+s2+s3...+...si+...+sn is the perimeter of the base, pB. Substituting in pB for s1+s2+s3...+...si+...+sn we find
the final form of the formula for the surface area of a right prism 2B+hpB
Properties of a Pyramid
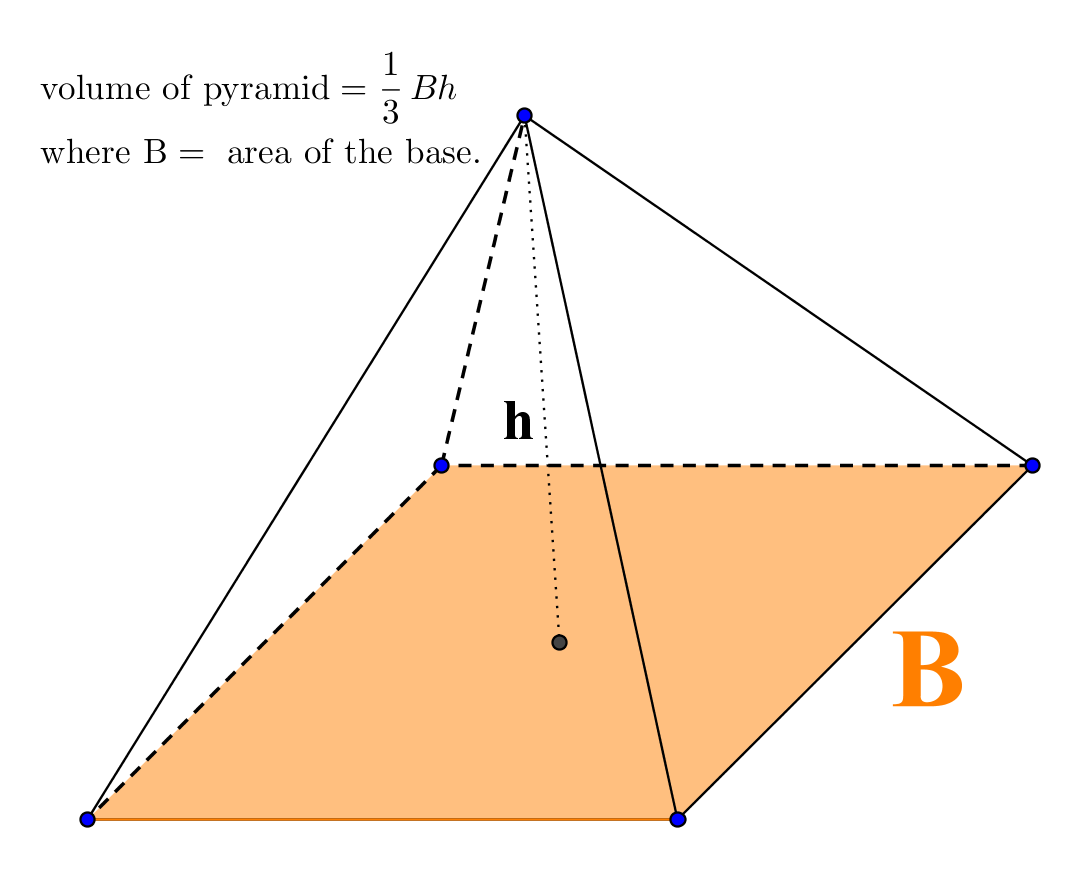
Volume of a Pyramid With A Regular Polygon as a Base
The volume of a pyramid is described by the formula
(1/3)Bh where B is the area of the base of the pyramid. This formula is a general formula for any pyramid, no-matter how many sides the base has, but be aware
that the formula for the area of the base will change depending on how many sides the base has. Pictured is a specific kind of pyramid, one with a square base. This pyramid has a more specific formula
that can be obtained by substituting the equation for the area of a square for B. If the sides of the base = a then the specific formula for a pyramid with a square base is (1/2)a2h.
For pyramids with more than four sides it is easiest to use the formula for a regular polygon Area(B)= (1/4)na2+cot(π/n) where n= number of sides on the polygon.
If we substitute this equation for B in the equation for the volume of a Pyramid with a regular polygon as a base we find (1/3)(1/4)na2+cot(π/n)h = (1/12)na2+cot(π/n) = Volume of a pyramid with a regular polygon as a base that has n sides .
Surface Area of a Pyramid With A Regular Polygon as a Base
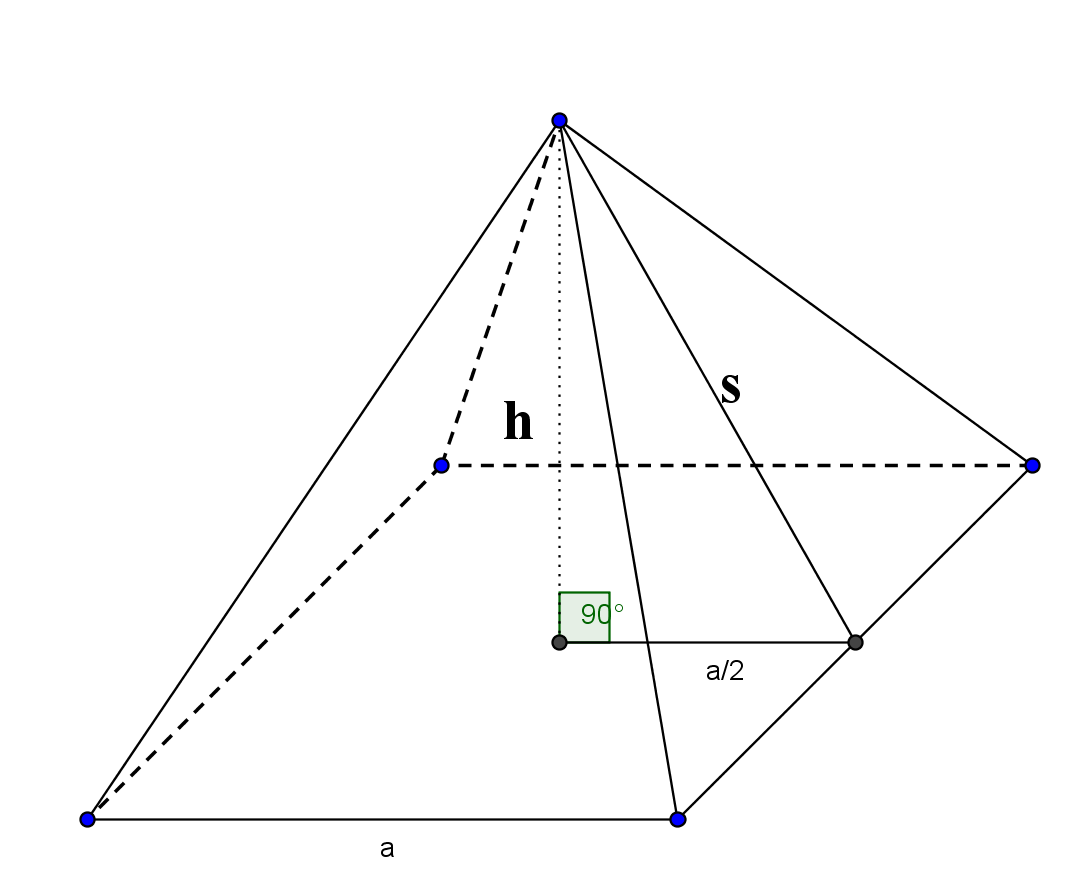To find the surface area of the pyramid we want to sum the areas of all of the faces of the pyramid. First, we have the area of the base, Area(B)= (1/4)na2+cot(π/n).
We also need the area of all of the triangular faces. When a pyramid has a regular n-gon as a base, it has n lateral-triangular faces all with equal area. The area for a triangle is (1/2) base* height. The lateral height of the triangle is different than the
height of the pyramid as a whole. We will label the lateral height of the triangles as s, for "slant height" to differentiate between the pyramid height and the triangles.
To find the slant height we can apply the Pythagorean theorem, as it is the hypotenuse of a right triangle with the sides h, and a/2, where a is the length of the base. Each of the lateral triangles of the pyramid have the area (1/2)as.
There are n triangles with equal area as lateral sides of the pyramid, so the total area of all of these triangles is (n/2)as. To find the total surface area of the pyramid we add the total area of all of the lateral sides with the area for the base of the triangle:
(n/2)as + (1/4)na2+cot(π/n).
Properties of a Cylinder
Volume of a Cylinder
The volume of a cylinder is similar to the volume of a rectangular prism in many ways. Most notably the formula for the volume of the cylinder is derived by multiplying the area of the base of the cylinder, πr2 by it's height, h.
The volume of a cylinder, πr2h, can be derived by using the method of exhaustion.
Surface Area of a Cylinder
The surface area of a cylinder is the sum of the two bases and the lateral surface area. There are two identical bases, both with area πr2.
The lateral surface area of the cylinder is the circumference of the cylinder 2πr multiplied by the height, h. The lateral surface area of a cylinder
can most easily understood as a rolled up rectangle with height, h, and width 2πr. Adding together the lateral area and the areas of the bases produces the
formula for the Surface area of a cylinder, 2πr2+2πr.
A visual representation of the surface area of a cylinder in Geogebra
Properties of a Cone
Volume of a Cone
The formula for the volume of a cone is 1/3 πr2h. The fist to discover this formula was Democritus. He did not proved a full proof of the formula but rather estimated it by observation. Eudoxus of Cnidus later
provided a full proof of the formula using the method of Exhaustion and the known formula for the volume of a pyramid. It is believed that Euclid's derivation of this formula in the 12th book of Euclid's elements is a version that can be originally attributed to Eudoxus of Cnidus.
Surface Area of a Cone
The surface area of a cone is characterized by the formula πrs+πr2where πrs is the lateral surface area of the cone and πr2 is the area of the base.
Properties of a Sphere
Volume of a Sphere
The discovery for the formula for the volume of a sphere is attributed to Archimedes of Syracuse. He did this two ways, first by the method of exhaustion made popular by Eudoxus of Cnidus, and then by a method that Archimedes devised himself
known as The Method of Mechanical Theorems.
Surface Area of a Sphere
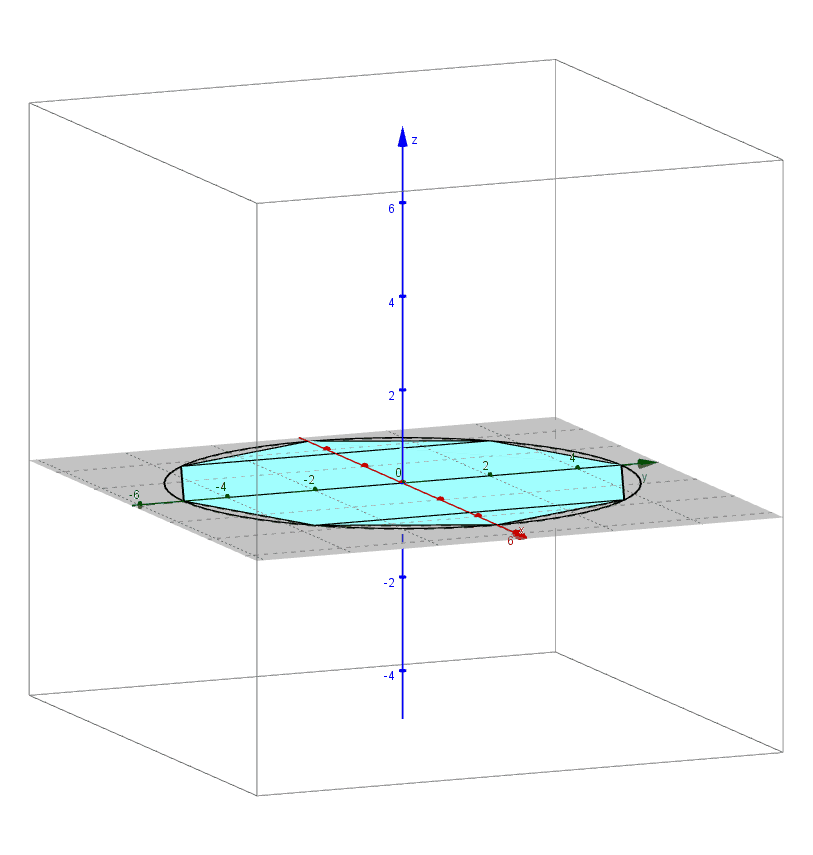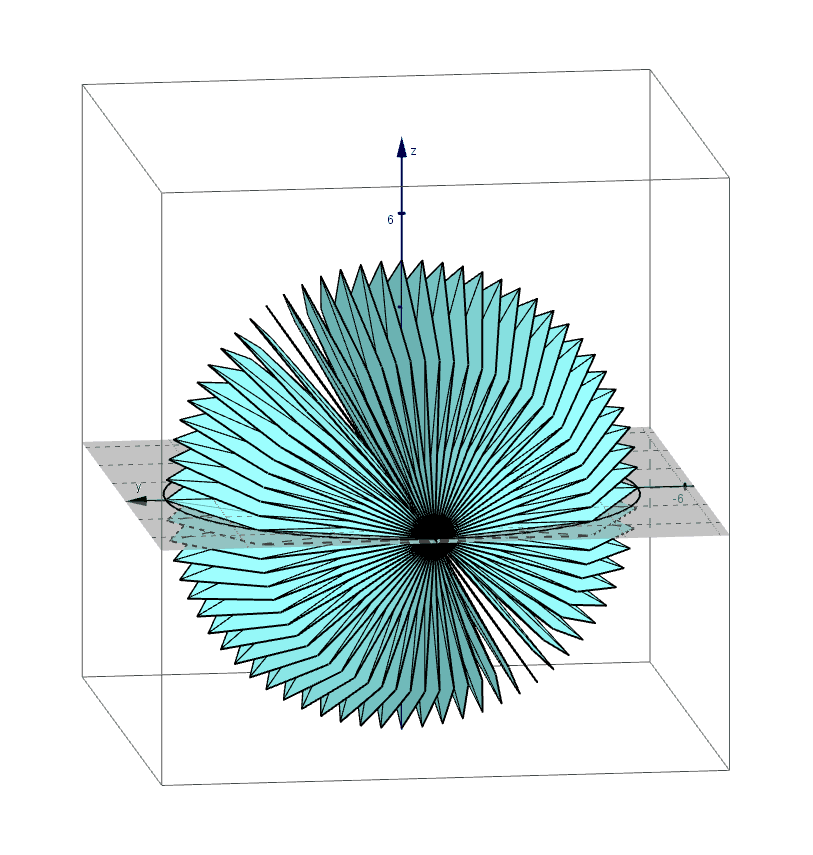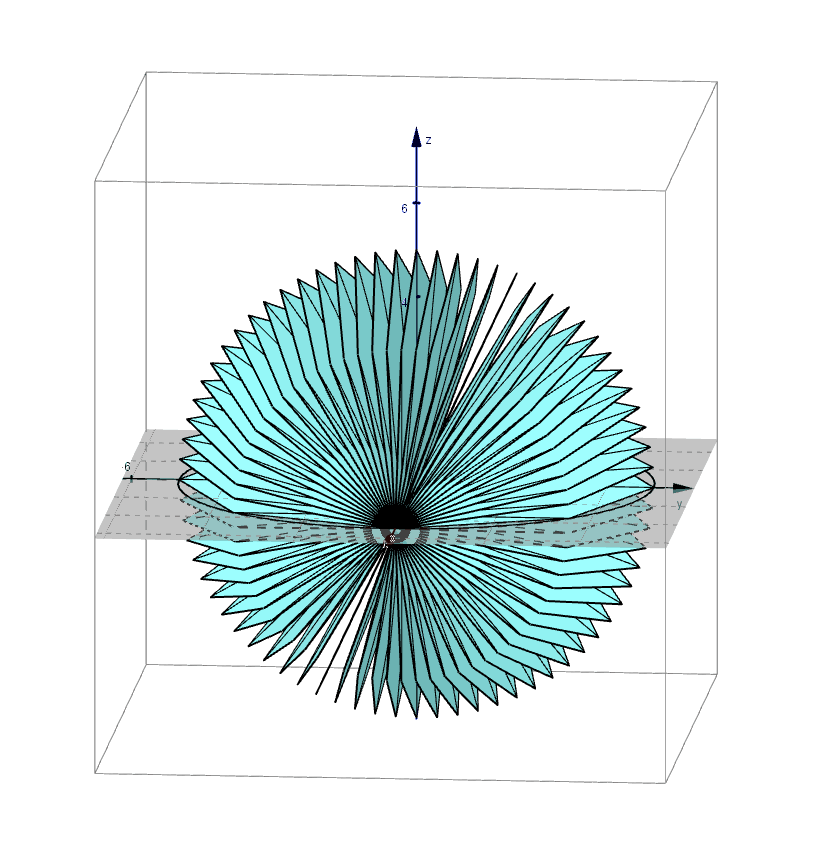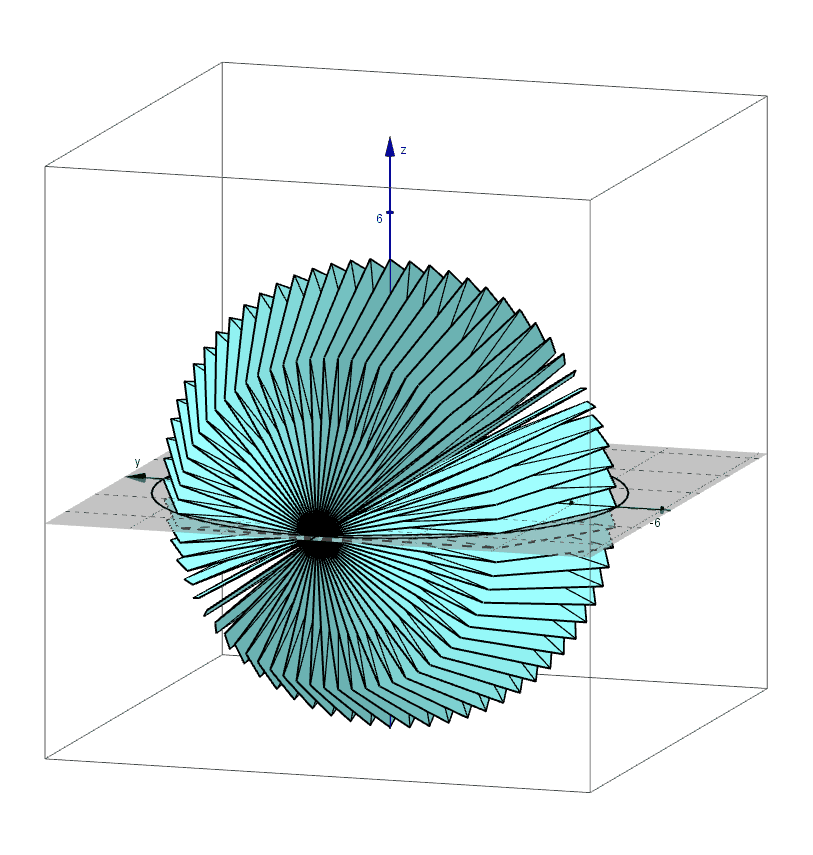
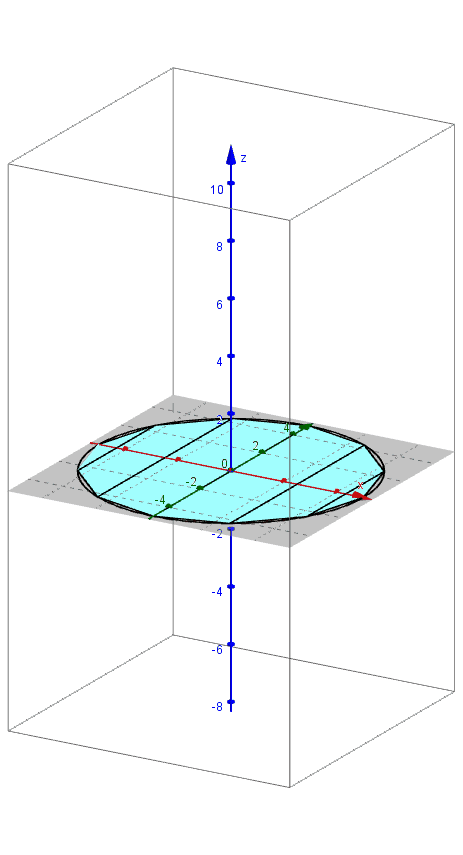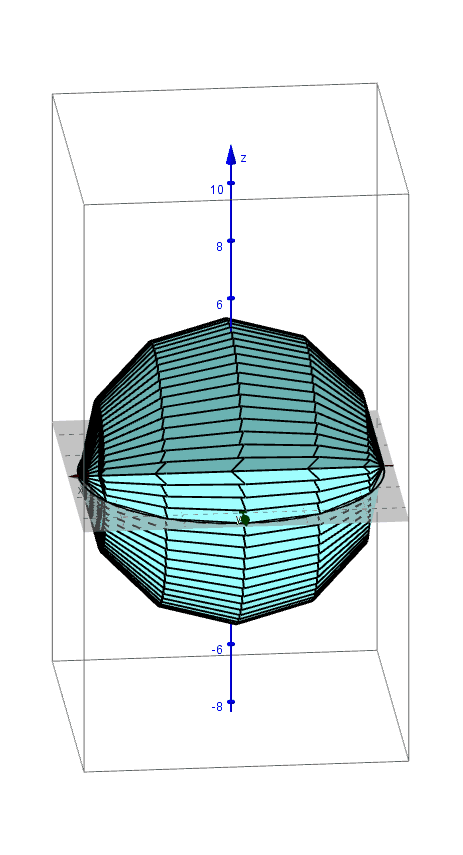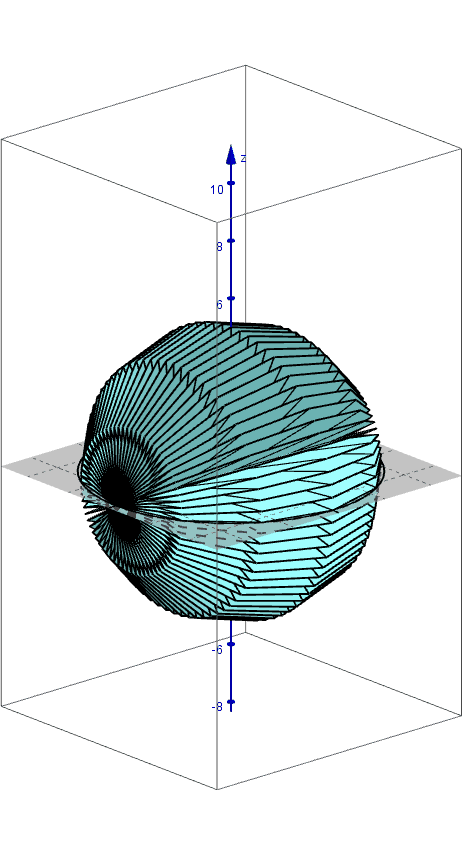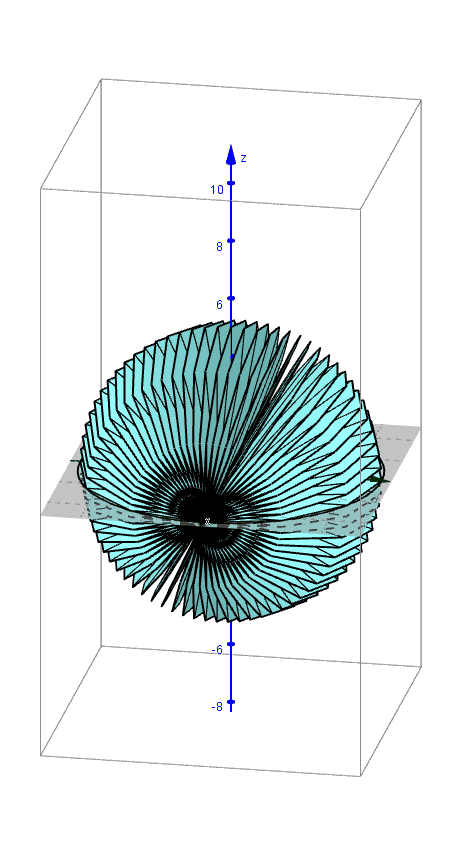
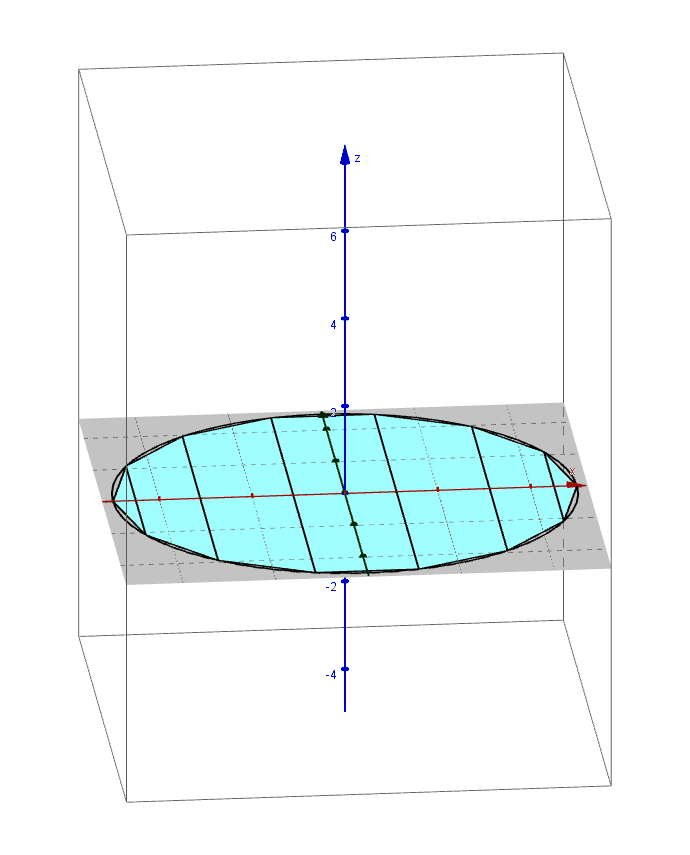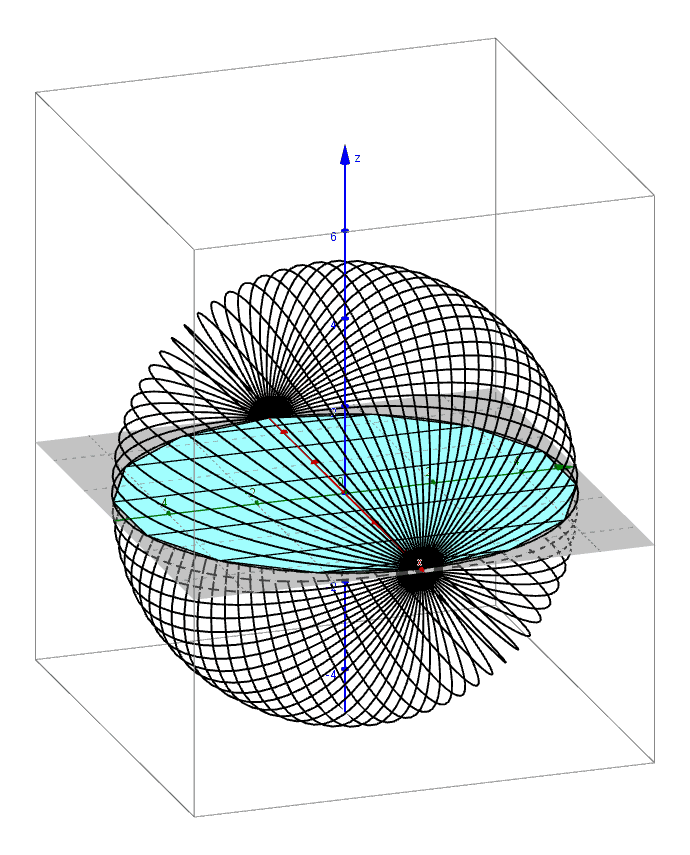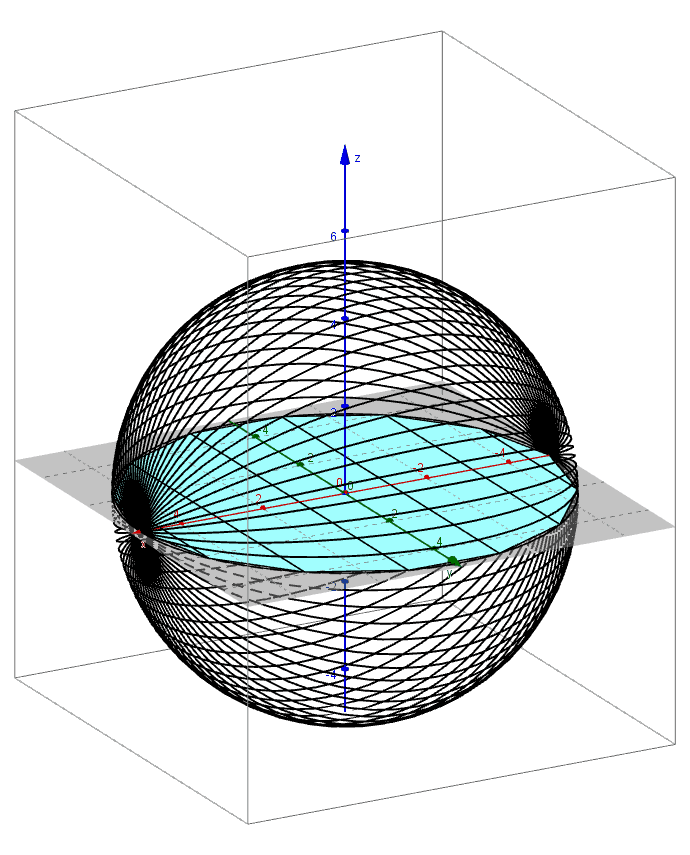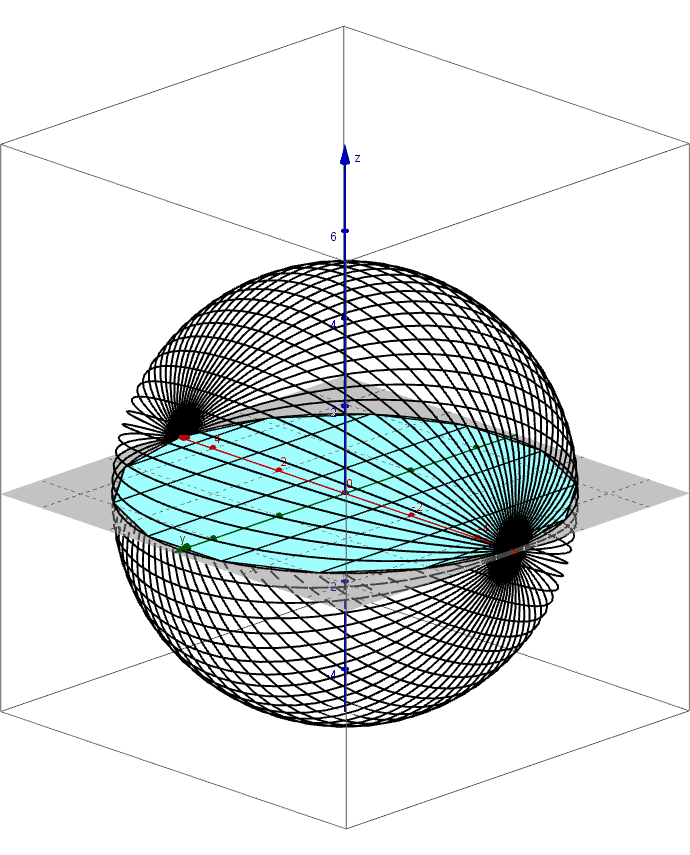
Archimedes found the formula for the volume of a sphere using the method of exhaustion. An applet that leads you through the derivation of this formula can be found here.
Pictured below are 3D renderings of the shapes that approximate a sphere using the method of exhaustion.
