As an introduction to the technique, below is a slightly trivial, but informative demonstration about how the method of exhaustion could be used to find the formula for the volume of a cylinder.
The method of exhaustion is a method for finding the area of a shape by inscribing regular polygons inside of it with an increasing number of sides. As the number of sides to the polygons increase the area of the polygons
converge to the area of the shape in which the polygons are inscribed. This method was made popular by Eudoxus of Cnidus in ancient Greece and quickly became the preferred form of proof for the area and volumes of objects. Archimedes has famously used this technique to
estimate π and find the surface area of a sphere.
As an introduction to the technique, below is a slightly trivial, but informative demonstration about how the method of exhaustion could be used to find the formula for the volume of a cylinder.

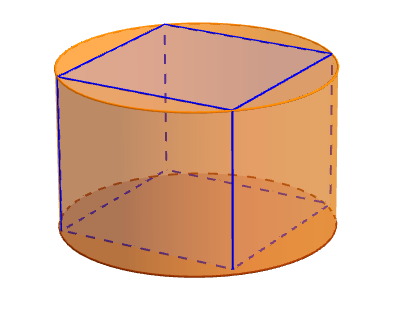
We begin with a prism inscribed inside a cylinder. The height of the prism and the height of the cylinder are equal.
The volume of the cylinder is equal to the area of the base multiplied by the height.
If we look at the cross section of the entire figure we find a polygon inscribed in a circle.
As the number of sides, n, of the polygon grows, the area of the polygon gets closer to the area of the circle.
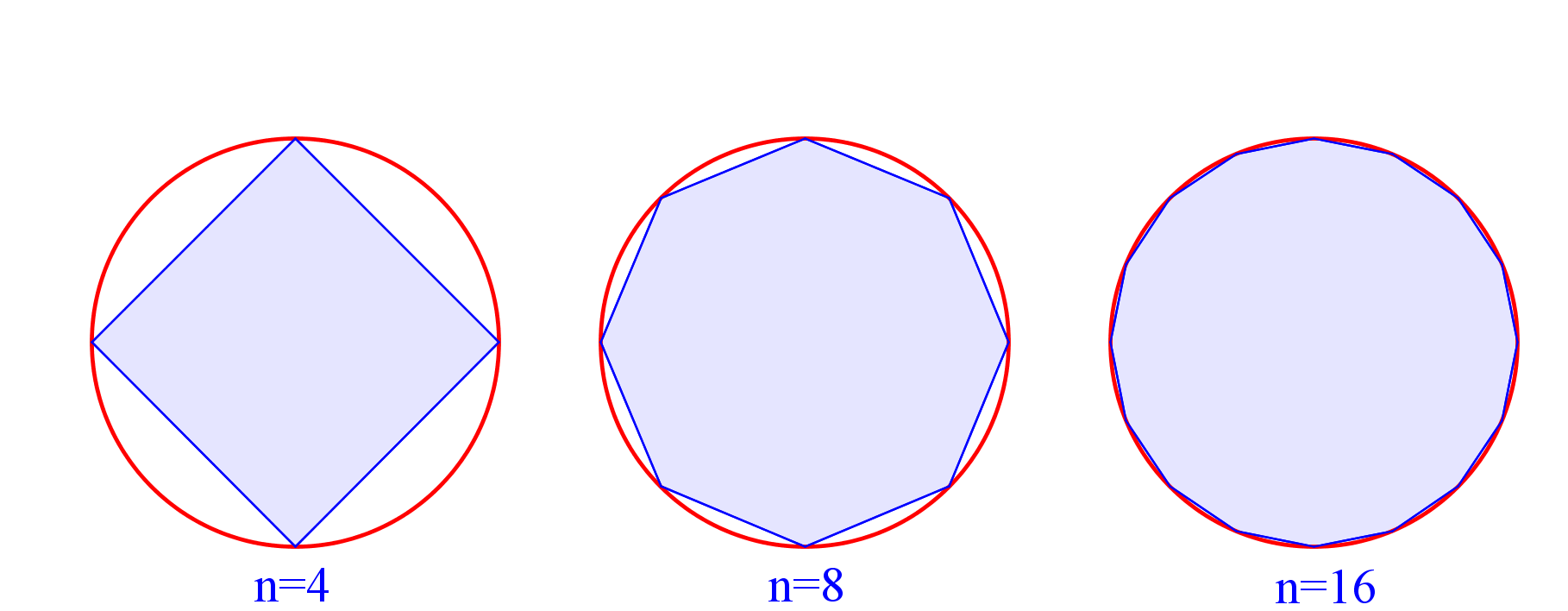
We know that area of the polygon will always be less than the area of the circle, because if it were not less than the circle it would not longer be able to be inscribed in the circle as the area of an inscribed figure is always less than the area of the figure circumscribing it.
Therefore we can say that the area of the polygon is limited by the area of the circle.
We can then substitute the formula for the area of a circle,