Background

In set theory, if the members of two sets can be matched up in a 1-1 correspondence, they are proven to have the same cardinality.

A set is ''denumerable'' if it can be set into 1-1 correspondence with N (the counting numbers)--it is ''countably infinite.'' Theoretically, one could count every element in a denumerable set.

Denumerable sets

To begin, consider the set of the even natural numbers. It is a proper subset of the set of N. Intuition tells us that a subset should be a smaller size than the set. Is it?

So our intuition was mistaken in that case. Now consider the integers. N is a subset of Z. What is the cardinality of the set of all integers?

And now, what about the rational numbers?

Thus far, we have seen that there are various sets that are countably infinite. Cantor called this new cardinal number representing the size of these sets ''ℵ₀'' (pronounced ''aleph-nought''). Is this the largest number? What could be bigger than the infinity of the counting numbers? But here comes the twist: not all sets are countably infinite.

Non-denumerable sets

Being uncountably infinite means that the cardinality of this set is greater than the cardinality of the denumerable sets. Believe it or not, there are more elements in this small interval than there are rational numbers! This next larger transfinite cardinal number is ''ℵ₁.''

Actually, any interval (a,b) has this same cardinality of ℵ₁ because all finite intervals can be matched in a 1-1 correspondence with the unit interval by the function y=a+(b-a)x. And so it is also possible to map the set of all real numbers, R, to the unit interval (0,1) with the function y= (2x-1) / (x-x²). Thus |R|=ℵ₁, and it is non-denumerable.

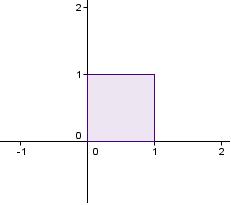
Consider the set of points contained in the square interval S above compared to the points in the interval between 0 and 1. For several years Cantor tried to prove that there is no 1-1 correspondence between the two sets before realizing that, actually, there is. First we need to know the following theorem: If |A| is less than or equal to |B|, and |B| is less than or equal to |A|, then |A|=|B|. So, consider the points in our two sets. We can easily match up any point k in the interval (0,1) with the ordered pair (k, 1/2) in the region S to show that |(0,1)| is less than or equal to |S|. Now consider the the ordered pairs of the points in the region. x and y are between 0 and 1, so x=0.a₁a₂a₃a₄...a_n... and y=0.b ₁b₂b₃b₄...b_n... . Now we simply associate each of these points with a point k in the interval, k=a₁b₁a₂b₂a₃b₃... . Thus |S| is less than or equal to |(0,1)|. So by our theorem, since |S| is less than or equal to |(0,1)| and |(0,1)| is less than or equal to |S|, |(0,1)|=|S|=ℵ₁.

Unions of sets

Let us now turn our attention to the irrational numbers. Suppose that the set of irrational numbers is denumerable. Consider then the union of the irrationals and the rationals. We already saw that Q is denumerable, so by our theorem, the union of these two sets is denumerable. But the union of the irrationals and the rationals is R, the real numbers, which we saw is non-denumerable. This contradiction arises because of the supposition that the irrationals are denumerable. Therefore, the set of irrational numbers must be non-denumerable.

As if that weren't surprising enough, Cantor also used this line of thinking to show that the transcendental numbers are also uncountably infinite, as opposed to the algebraic numbers which are only countably infinite. That means that the transcendental numbers, which are so hard to come by, vastly outnumber the algebraic numbers with which we are quite familiar. Once again, our intuition has let us down.

Note: According to the Zermelo-Fraenkel set theory with the axiom of choice, ℵ₁=2^{ℵ ₀}. However, this can neither be proven nor disproven within that system.

Even greater cardinals

A power set P[S] is the set of all subsets of a given set S. One of Cantor's theorems states that |A| is less than |P[A]|. So |(0,1)| is less than |P[(0,1)]|, which means that there is a transfinite cardinal greater than ℵ₁, call it ℵ₂. And we can continue taking power sets to generate more cardinals (ℵ₃, ℵ₄, ℵ₅, etc). Another of Cantor's theorems tells us that we could continue this process indefinitely; in other words, there is no greatest transfinite number.

Operations of transfinite numbers

The Continuum Hypothesis

During the latter part of his life, Cantor tried to prove his hypothesis that there are no other transfinite cardinals between ℵ₀ and ℵ₁. He never succeeded in his endeavor. In 1940, Gödel proved that the hypothesis couldn't be disproved, and in 1963 Cohen proved that it cannot be proved either. So the hypothesis is like a postulate that we can choose to adopt as true or not.