The Golden Ratio: φ
Background on the Golden Ratio:
The golden ratio is a numerical constant, similar to π and e. Its numerical value is (1+√5)/2 or approximately 1.61803398875… and is
usually denoted by the Greek letter phi, φ. The golden ratio is irrational and is sometimes considered to be more irrational than other
irrational numbers. This is because there exists no rational number that closely approximates φ, like 22/7 = 3.14285714... approximates π =
3.141592654... and 19/7 = 2.714285714... approximates e = 2.71281828... (MathIsFun.com, 2011).
The golden ratio has many names: the golden section, the golden mean, the golden cut, the divine proportion, along with many others (Dunlap, 2003,
p. 1). The idea behind the golden ratio originates in Euclidean geometry, but may have been known by the ancient Greeks and Egyptians (Debnath, 2011,
p, 343). It has been used by many different mathematicians throughout history. Greek mathematicians referred to this ratio as the “division of a line
in mean and extreme ratio,” which is stated by Johannes Kepler, a brilliant German mathematician, in the following quote:
“Geometry has two great treasures: one is the theorem of Pythagoras; the other,
the division of a line in extreme and mean ratio. The first we may name as a
measure of gold, the second we may name as a precious jewel.” (Debnath, 2011, p. 342)
The golden ratio appears in Euclid’s Elements, Book VI as the solution to Proposition 30 which states “To cut a given
finite line in extreme and mean ratio” (Falbo, 2005, p. 124). This is achieved by “dividing a line segment AB = a by the point C
[…] into two unequal parts x and y(<x) in such a way that the ratio of the larger part x to the smaller part y is equal
to that of the total length x+y(=a) to the larger segment x” (Debnath, 2011, p. 342). This statement yeilds equal ratios represented in
the following:
x/y = (x+y)/x = 1 + y/x.
Manipulation yeilds the following quadratic:
(x/y)^2 - (x/y) - 1 =0.
Using the quadratic formula, (x/y) = (1/2)(1+√5) = φ (Debnath, 2011, p. 343). Thus, we see how the value of φ was determined mathematically.
Constructing segment with points that satisfy the golden ratio can be done in a simple manner. I created a GeoGebra applet that can be used to do this. The steps come from the Falbo article, page 125. This applet
creates a golden ratio in the 1st dimension. Similar constructions can be made in the 2nd and 3rd dimensions (see Stuart, 2006, p. 61-63).

Back to the top
Properties of the Golden Ratio:
The golden ratio “seems to infiltrate just about every aspect of mathematics” (Posamentier & Lehmann, 2011, p. 4). I have included
five different mathematical properties here that show how φ does this. First, when 1 is subtracted from φ, the result is the reciprocal of
φ, or 1/φ, which is 0.618033… Second, φ can be written as a continued fraction and endless square root
(Falbo, 2005, p. 133). These are as follows:

A third interesting property of φ is its relation to the Fibonacci numbers. The numerical value of fractions created by
sequential numbers in the Fibonacci sequence, the larger as the numerator, approaches φ (Hyde, 2004, p. 30). Even if the
first two numbers are not 1 and 1 (or 0 and 1), the ratio still approaches φ. A
NLVM applet
shows this process. Fourth, golden ratios appear in regular pentagons whose side length is 1. I created another
GeoGebra applet that shows this property. Finally, when creating golden rectangles inside of each other, as appears in the figure below,
the sum of the areas is φ^2 (Falbo, 2005, p. 130-131).

It is important to note that φ is no the only number that has these particular properties. However, φ is unique in that when
formulas are determined for these properties, the variables equal φ or 1 (see Falbo, 2005, p. 129-133).
This webpage done by Wolfram MathWorld and this
webpage done by MathIsFun.com contain even more properites of and information about the Golden Ratio.
Back to the top
The Golden Spiral:
The golden spiral is a logarithmic curve constructed around the golden ratio. I created a third GeoGebra
applet that creates a golden curve from a golden rectangle. Similar curves can be created at different ratios, such as 1/3 or √2. The
following is a picture of the golden curve:

Other golden shapes also exist. As stated earlier, there exist golden rectangles. The sides of these rectangles have the ratio of φ. There also
exist various forms of golden triangles. These satisfy the condition that "when a triangle similar to it is removed from the golden triangle, the
ratio of the golden triangle to that of the remaining triangle is equal to the golden ratio" (Debnath, 2011, p. 344). These triangles can be right
triangles or isoceles trianges. Specifically, an isoceles triangle is a golden triangle if each of its base angles measure 72° (Debnath, 2011,
p. 345). There also exists a "golden quadratic equation" whose positive root is φ: φ^2 - φ - 1 = 0 (Debnath, 2011, p. 343).
Back to the top
The Golden Ratio in the World:
The golden ratio has some appearance in nature. It appears in the growth of pinecone or sunflower seeds and plants in general. Each new seed or leaf grows offset
from the previous one at an angle of 2π/φ (Hyde, 2004, p. 30). The YouTube clip “Doodling in Math Class: Spirals, Fibonacci, and Being a Plant Part [2 of 3]” explains why this may occur (Vihart, 2012).
It has been previously believed that the golden spiral appeared in sea shells. However, finding a sea shell whose spiral matches the golden spiral is quite rare.
Sea shells spirals tend to fit a 1.33:1 ratio rather than 1.618:1 ratio (Falbo, 2005, p. 127). The ratio across the shell usually fits the ratio, but the spiral
itself may not (Phi: The Golden Number, 2012).


It is believed by many architects and artists that “rectangles with sides in [the golden ratio] offer the most pleasing aspect
ratio” (Hyde, 2004, p. 30). They also believe that “the golden ratios are not only pleasing of all proportions, but also enhance beauty in
art and paintings” (Debnath, 2011, p. 350). This idea gives meaning to the quote from John Keats' "Ode on a Grecian Urn":
"Heard melodies are sweet, but those unheard
Are sweeter." (Stuart, 2006, p. 64)
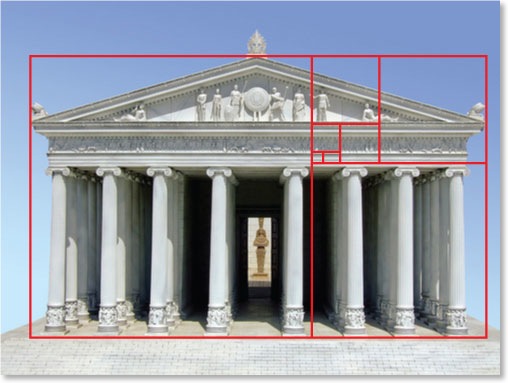
In many architectural works and paintings, the golden ratio can be discovered. Such examples are the Parthenon, the Great Pyramids of Giza,
the Mona Lisa and the Bathers at Asniéres. The following pictures show how these ratios appear:



The golden ratio can also be found in the human body and face. Measurements of different parts of the body reflect the golden ratio. Examples are total
height to the distance from the top of the head to the end of the fingers and length of the forearm to the length of the hand. Even more examples
can be found at this website.

The golden ratio can also be found in other living creatures as the pictures below indicate:


Back to the top
References and Resources:
Debnath, L. (2011). A short history of the Fibonacci and golden numbers with their applications. International Journal Of Mathematical Education In Science & Technology, 42(3), 337-367. doi:10.1080/0020739X.2010.543160
Divine Ratio 3 [JPeg]. (2010). Retrieved November 23, 2012 from: http://predella.wordpress.com/2010/10/04/divine-proportions-golden-ratio-set-dressing/.
Dunlap, R. (2003). The golden ratio and Fibonacci numbers. Singapore: World Scientific Publishing Co. Pte. Ltd.
Falbo, C. (2005). The golden ratio: A contrary viewpoint. The College Mathematics Journal, 36(2), 123-134.
The Great Pyramid of Khufu or Cheops [Edited photograph]. (2010). Retrieved November 23, 2012 from: http://catphi.wordpress.com/2010/09/16/fibonacci-sequence/.
Golden Rectangles [Clip Art]. (2012) Retrieved November 23, 2012, from: http://etc.usf.edu/clipart/42900/42987/golden7_42987.htm.
Golden Spiral [JPeg]. (2010) Retrieved November 23, 2012, from: http://en.allexperts.com/q/Advanced-Math-1363/2010/5/math-229.htm.
Hyde, H. (2004). The golden ratio. Australian Mathematics Teacher, 60(1), 30-31.
Livio, M. (2002). The golden ratio: The story of phi, the world’s most astonishing number. New York, NY: Broadway Books.
Posamentier, A. S., & Lehmann, I. (2011). The glorious golden ratio. Amherst, NY: Prometheus Books.
Stuart, S. (2006). Golden sections. Australian Senior Mathematics Journal, 20(1), 60-64.
Tong, J. & Kung S. (2007). A simple construction of the golden ratio. Forum Geometricorum, 7, 31-32.
[Untitled image of a dolphin with golden proportions]. Retrieved November 26, 2012 from: http://jwilson.coe.uga.edu/EMT668/EMAT6680.F99/Hekimoglu/emat6700/golden%20ratio/animalgold.html
[Untitled image of Georges Seurat's Bathers at Asniéres with golden rectangle overlay]. Retrieved November 23, 2012 from: http://www.goldennumber.net/art-composition-design/.
[Untitled image of golden ratios on a line]. Retrieved November 26, 2012 from: http://www.mathsisfun.com/numbers/golden-ratio.html
[Untitled image of a human face with golden proportions]. Retrieved November 26, 2012 from: http://artspilesenglish.blogspot.com/2012/05/golden-proportion-in-any-face.html
[Untitled image of the Parthenon with golden rectangles]. Retrieved November 23, 2012 from: http://www.rangecookers.co.uk/files/golden_ratio_cooker_design.html
[Untitled image of a tiger with golden proportions]. Retrieved November 26, 2012 from: http://techcenter.davidson.k12.nc.us/group2/nature.htm
Back to the top













