class Web Page
Main
Assignments
Knowing the area and volume of shapes has many practical uses in our day to day lives. Whether the concept in question has to do with knowing how much paint to buy for a wall, how much grain to buy to plant a field, how much concrete to buy for a project, or knowing how much hay to fill a barn. Many shapes we deal with on a day to day basis have known formulas such as triangles, rectangles, rectangular prisms, or pyramids. What happens when you have an irregular shape or a shape similar to a known shape but has been distorted? Maybe you may find Cavalieri's Principle to be of some benefit.
Before diving into what Cavalieri's Principle actually entails, you may be wondering who even is Cavalieri? Well Bonaventura Cavalieri was born in Milan Italy in 1598. His interest in mathematics was heavily influenced by two things. The first being the book Euclid’s Elements and a meeting that he had with Galileo Cavalieri Applied to be the chair of mathematics at several Universities but was rejected many times due to him being too young and because his religious beliefs were looked down on. When Cavalieri finally did become a professor of mathematics wrote his method of indivisibles. This method works to find the area of geometric shapes similar to integral calculus, which was a precursor to the Cavalieri principle. Cavalieri put off publishing his method of indivisibles for 6 years because Galileo was working on a similar topic and he didn’t want to steal his thunder. When Cavalieri finally published his work on indivisibles it was put under scrutiny and rejected by scholars. Later Cavalieri would write "Six Geometrical Exercises'' where he better explained his ideas. After this publication his ideas finally started to catch on. “In Cavalieri’s day his method was controversial [because] it was not justified with a rigorous proof. In spite of this many mathematicians including Galileo thought it was a great idea. Today, we can rigorously justify his principle using real analysis.”(AITKEN pg1.)
Cavalieri's principle states that for any two three-dimensional objects have the same height and cross-sectional area over that entire height, they will have the same volume.
In the context of 2D shapes, Cavalieri's Principle states that if two plane regions (two-dimensional shapes) have the same height and for any pair of parallel lines perpendicular to the height, the lengths of the segments intercepted by the regions are always equal, then the two regions have the same area.
you might be asking yourself what does that mean.
look at the 4 shapes below. what can you say for sure about them?

I can tell you that they all have the same area and you might believe me but how can you prove to yourself that this is the case?
Use the applet below to hopefully convince yourself that this is in fact the case.
While using the Applet above hopefully you have seen how Cavalieri's principle applies in two dimentions below is a link to an applet created by Khan Academy which shows an example of how Cavalieri's principle applies in 3D (just so you know what to do drag your mouse up and down by the left cone)
Super awesome to Khan Academy(this will open in a new tab)
Ok now that you have played with this applet you should have a pretty good idea of how this principle works in 3D. while Using the Applet above you may have noticed that if you were to cut each of the object at the same height the shape formed is exactaly identical. this is true for every height thus the two shapes have the exact same volume.
A very important thing to note is that the cross sections at any given height do not actually need to be the same shape. As long as the crosssections have the same area for every height the two shapes have the same volume
Probably the most basic example of this principle relates a cylinder to a rectangular prism. A rectangular prism with the given dimensions of 3,3,5 and a cylinder with a height of 5 and a radius of 3/√(π) we can use the equations to show that the 2 shapes have the same volume 3*3*5 = 45 or 5π(3/√(π))2=5*9= 45.
Another valid way for us to show that the two shapes have the same volume is to use Cavalieri's Principle. If we put the two shapes side by side so that the height is 5 for each shape. In regards to the cylinder for every possible cross section parallel to the base of the cylinder we get a circle with radius 3/√(π) The area of any of these particular cross sectioned circles is 9 units squared. For the rectangular prism each cross section defined the same way as we defined it for the cylinder will give a 3 by 3 square which has an area of 9 units squared.
thus we can rightly make the claim: because the two shapes have the same height and for every cross section parallel to the base the two shapes always have the same area therefore the two shapes must also have the same volume by virtue of Cavalieri's Principle.
The area for any given cone is (1/3)*base*height. where base is simply the area of the base. We can know confidently that every cone follows this equation using Cavalieri's Principle. to show that any cone with the same height and the same base area will have the same volume is actually a simple matter. Given any cone with a base of area b and a height of h we can find the scaling factor at any height. The scaling factor equals (h-k)/h where k is the height of the cross section(I'm not going to go into to much detail about scaling that is a topic for another day). The formula for the area of any scaled shape equals (the area of the original shape) *(the scale Factor)2 therefore the area of any given cross section normal to the height and parallel to the base at height k is: (b(h-k))2/(h2). because the shape of the base has no effect on the formula for scaling we can use Cavalieri's Principle to conclude that the formula for any cone is bh/3.
Some of the uses of this principle is finding volume or area of shapes for which there is no formula. This can help with planning, making estimates, it can also be used to compare integrals of strange equations. Cavalieri's principle works in a similar manner to a jacobian which is used to simplify integration by shifting the coordinates to better understood coordinates or where it will be simpler to solve for.
Romans Paper: Cavalieri's Principle.pdf
Cavalieri's Principle
Introduction
Knowing the area and volume of shapes has many practical uses in our day to day lives. Whether the concept in question has to do with knowing how much paint to buy for a wall, how much grain to buy to plant a field, how much concrete to buy for a project, or knowing how much hay to fill a barn. Many shapes we deal with on a day to day basis have known formulas such as triangles, rectangles, rectangular prisms, or pyramids. What happens when you have an irregular shape or a shape similar to a known shape but has been distorted? Maybe you may find Cavalieri's Principle to be of some benefit.
History
Before diving into what Cavalieri's Principle actually entails, you may be wondering who even is Cavalieri? Well Bonaventura Cavalieri was born in Milan Italy in 1598. His interest in mathematics was heavily influenced by two things. The first being the book Euclid’s Elements and a meeting that he had with Galileo Cavalieri Applied to be the chair of mathematics at several Universities but was rejected many times due to him being too young and because his religious beliefs were looked down on. When Cavalieri finally did become a professor of mathematics wrote his method of indivisibles. This method works to find the area of geometric shapes similar to integral calculus, which was a precursor to the Cavalieri principle. Cavalieri put off publishing his method of indivisibles for 6 years because Galileo was working on a similar topic and he didn’t want to steal his thunder. When Cavalieri finally published his work on indivisibles it was put under scrutiny and rejected by scholars. Later Cavalieri would write "Six Geometrical Exercises'' where he better explained his ideas. After this publication his ideas finally started to catch on. “In Cavalieri’s day his method was controversial [because] it was not justified with a rigorous proof. In spite of this many mathematicians including Galileo thought it was a great idea. Today, we can rigorously justify his principle using real analysis.”(AITKEN pg1.)
Explination of Mathamatics
Cavalieri's principle states that for any two three-dimensional objects have the same height and cross-sectional area over that entire height, they will have the same volume.
In the context of 2D shapes, Cavalieri's Principle states that if two plane regions (two-dimensional shapes) have the same height and for any pair of parallel lines perpendicular to the height, the lengths of the segments intercepted by the regions are always equal, then the two regions have the same area.
you might be asking yourself what does that mean.
look at the 4 shapes below. what can you say for sure about them?

I can tell you that they all have the same area and you might believe me but how can you prove to yourself that this is the case?
Use the applet below to hopefully convince yourself that this is in fact the case.
Cavalieri's principle in two dimensions
While using the Applet above hopefully you have seen how Cavalieri's principle applies in two dimentions below is a link to an applet created by Khan Academy which shows an example of how Cavalieri's principle applies in 3D (just so you know what to do drag your mouse up and down by the left cone)
Super awesome to Khan Academy(this will open in a new tab)
Ok now that you have played with this applet you should have a pretty good idea of how this principle works in 3D. while Using the Applet above you may have noticed that if you were to cut each of the object at the same height the shape formed is exactaly identical. this is true for every height thus the two shapes have the exact same volume.
A very important thing to note is that the cross sections at any given height do not actually need to be the same shape. As long as the crosssections have the same area for every height the two shapes have the same volume
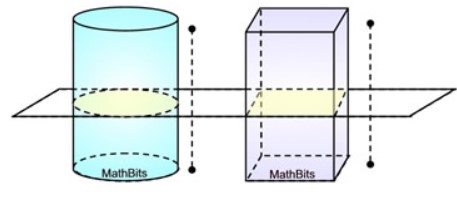
Probably the most basic example of this principle relates a cylinder to a rectangular prism. A rectangular prism with the given dimensions of 3,3,5 and a cylinder with a height of 5 and a radius of 3/√(π) we can use the equations to show that the 2 shapes have the same volume 3*3*5 = 45 or 5π(3/√(π))2=5*9= 45.
Another valid way for us to show that the two shapes have the same volume is to use Cavalieri's Principle. If we put the two shapes side by side so that the height is 5 for each shape. In regards to the cylinder for every possible cross section parallel to the base of the cylinder we get a circle with radius 3/√(π) The area of any of these particular cross sectioned circles is 9 units squared. For the rectangular prism each cross section defined the same way as we defined it for the cylinder will give a 3 by 3 square which has an area of 9 units squared.

(this photo is taken from https://mathbitsnotebook.com/Geometry/3DShapes/3DCavalieriPractice.html)
(this photo is taken from https://mathbitsnotebook.com/Geometry/3DShapes/3DCavalieriPractice.html)thus we can rightly make the claim: because the two shapes have the same height and for every cross section parallel to the base the two shapes always have the same area therefore the two shapes must also have the same volume by virtue of Cavalieri's Principle.
The area for any given cone is (1/3)*base*height. where base is simply the area of the base. We can know confidently that every cone follows this equation using Cavalieri's Principle. to show that any cone with the same height and the same base area will have the same volume is actually a simple matter. Given any cone with a base of area b and a height of h we can find the scaling factor at any height. The scaling factor equals (h-k)/h where k is the height of the cross section(I'm not going to go into to much detail about scaling that is a topic for another day). The formula for the area of any scaled shape equals (the area of the original shape) *(the scale Factor)2 therefore the area of any given cross section normal to the height and parallel to the base at height k is: (b(h-k))2/(h2). because the shape of the base has no effect on the formula for scaling we can use Cavalieri's Principle to conclude that the formula for any cone is bh/3.
Significance and applications
Some of the uses of this principle is finding volume or area of shapes for which there is no formula. This can help with planning, making estimates, it can also be used to compare integrals of strange equations. Cavalieri's principle works in a similar manner to a jacobian which is used to simplify integration by shifting the coordinates to better understood coordinates or where it will be simpler to solve for.
Romans Paper: Cavalieri's Principle.pdf