Introduction
Many people hate math because they think that there are no practical applications of it, but what they don't know is that there is math everywhere, including some childhood toys. The spirograph, a common childhood toy involving two gears that rotate around each other to create pretty pictures, is one of these toys. In fact, math is a big aspect of this toy. When kids play with a spirograph and experiment by trying different combinations, it can help them develop mathematical and scientific intuition by realizing patterns, hypothesizing, testing, and reaching conclusions (Aydemir, 2020). There are many different mathematical aspects to the spirograph including application of the least common multiple, trigonometry, geometry, and modular arithmetic. Many of these concepts build off of the Utah common core standards for middle school and high school students.
Background
To understand the math behind spirographs, it is essential to first look at the history behind them. It hasn't been determined who exactly came up with the idea of the spirograph, but there are many different people who had influences on its invention.
One of these people was a Greek architect and engineer named Peter Hubert Desvignes. In 1827 he invented a device called a "speiragrah" that was created to produce spiral drawings and used to prevent forgeries on banknotes (Evans, 2021).

Another person who had an influence on the spirograph invention was Bruno Abakanowicz, a mathematician who invented a spirograph between 1881 and 1900 that was used by engineers to calculate an area that was delimited by curves (Evans, 2021). The spirograph toy was first introduced in 1907 with the idea of a Wondergraph. This toy was made of wood and a contraption that helped the pen spin around and create symmetrical drawings.

While there are many historical inventions of a spirograph like contraption, the spirograph toy that is known today was an invention of Denys Fisher in 1962. It was originally developed as a drafting tool that was created by meccano pieces, but because of influence from friends and family he marketed it as a toy in the early 60s (Coopee, 2023). Since then, many different spirograph applets have been created and they have become widely available.

Explanation of Mathematics
As previously mentioned, there are many different mathematical aspects of the spirograph. One of the main ones is the application of trigonometric concepts. The trigonometric relationships behind spirographs is an extension of trigonometry learned in secondary education. Spirographs can be described mathematically by finding their parametric equations. Consider the following figure by Juergen Koeller.
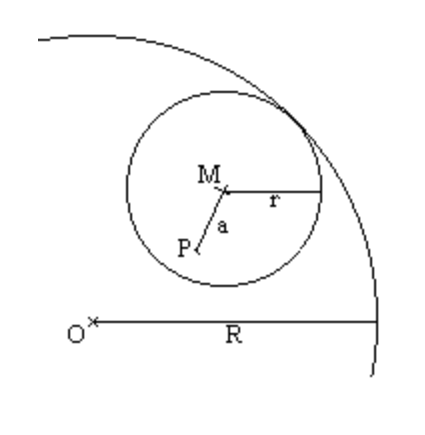
In this figure, R represents the radius of the big circle and is a fixed value. P also represents a fixed value that has distance a from the center M of the small circle. P can be any of the holes on the small rotating circle. Also, r represents the radius of the small circle. When the small circle is being rotated, we follow the point P. The following parametric equations represent the movement of the point with x and y being the coordinates of point P depending on the angle t. No matter where P is, R and r always stay constant (Koeller, 2000).

Another mathematical concept behind the spirograph is geometry. There are different forms of geometrical shapes made by spirographs and these are influenced by the location of the pen hole. First, if the pen hole is at the center of the small circle, the curve made will simply be a circle centered at the center of the big circle. If the pen hole is at the edge of the small circle it will create a shape with a set of curves that bounce off the edges of the big circle and create pointed curves. This shape is called a hypocycloid (Steckles, 2022). The following figure shows an example of these.
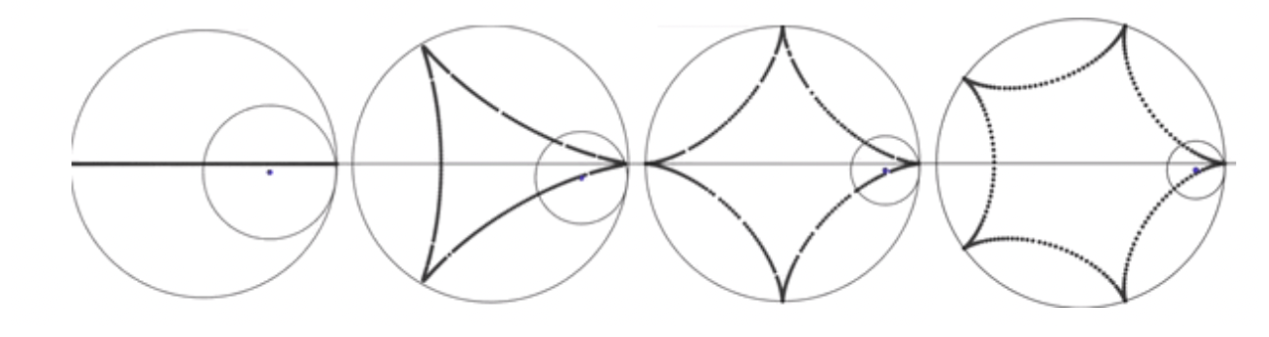
If the pen hole isn’t in the center or on the edge, then it is dependent on r/R and P. This then creates a type of shape called hypotrochoids that may be various shapes. Some may be similar to a circle and some similar to a hypocycloid. Here is an example of this shape.

There are also some formulas that can determine how many petals (the outside points of the spiral) a shape has and how many rotations are needed to close a shape based on the number of teeth of the inside and outside gears. Least common multiple and modular arithmetic are both mathematical concepts that are used in these formulas. These ideas build off of the idea of least common multiple that is learned in eighth grade and arithmetic with polynomials which is learned in Secondary Math III. The number of petals N can be modeled by the formula N=LCM(R,W)/R where R is the number of teeth on the rotating disc and W is the number of teeth on the wheel (Rusenko, et al.). The number of rotations can be modeled by N= Z_x,ord (y)(y/x) where x is the number of teeth on the wheel and y is the number of teeth on the rotating disc (Brown, 2008).
This applet helps students explore the parametric equations of spirographs and how different parts of the equations create hypotrochoids and hypocycloids.
Applications/Significance
Spirographs have many applications, but with today’s technology a lot of them are outdated. Today we have computers that can generate any curves and allow for better exploration (Shell-Gellasch, 2018). However, in the late 19th and early 20th centuries spirographs were used for educational purposes and were great teaching devices. The mathematical concepts behind spirographs can also be used in engineering and art and design. Also, spirographs and spirograph applets can be used in secondary schools to explore these concepts and introduce students to different math related technologies.
References
Aydemir, E. (2021, July 26). Spirograph. Math Fan. https://www.mathcuriosity.com/post/spirograph
Brown, D. (2008, November 13). Spirographs: An application of Modular Arithmetic. The Math 152 Weblog. https://math152.wordpress.com/2008/11/13/spirographs-an-application-of-modular-arithmetic/
Coopee, T. (2023, September 14). Spirograph from Kenner (1967). Toy Tales. https://toytales.ca/spirograph-from-kenner-1967/
Evans, R. (2021). The history of Spirograph. Spirograph Girl. https://www.spirographgirl.com/blog/the-history-of-spirograph
Kaveney, W. (2004b). The Marvelous Wondergraph. CONTENTdm. https://www.digitalindy.org/digital/collection/tcm/id/787/
Koeller, J. (2000). Spirograph. https://www.mathematische-basteleien.de/spirographs.htm#:~:text=The%20trigonometric%20formulas%20guarantee%20periodical,the%20periodicity%20
of%20the%20drawings.&text=If%20you%20use%20a%20program,get%20the%20so%2Dcalled%20hypocycloids.&text=T
he%20parameter%20a%20is%20different%20for%20each%20picture.
Rusenko, D., Veltri, D., & Fanini, C. (n.d.). The math of spirographs. Mathematics Teaching and Learning. http://mathadinfinitum.weebly.com/the-math-of-spirographs.html
Shell-Gellasch, A. (2017, March 17). The Spirograph and kinematic models: Making math touchable (and pretty). National Museum of American History. https://americanhistory.si.edu/blog/2014/03/the-spirograph-and-kinematic-models-making-math-touchable-and-pretty.html
Steckles, K. (2022, December 21). The Mathematics of Spirograph. The Aperiodical. https://aperiodical.com/2021/12/the-mathematics-of-spirograph/
Many people hate math because they think that there are no practical applications of it, but what they don't know is that there is math everywhere, including some childhood toys. The spirograph, a common childhood toy involving two gears that rotate around each other to create pretty pictures, is one of these toys. In fact, math is a big aspect of this toy. When kids play with a spirograph and experiment by trying different combinations, it can help them develop mathematical and scientific intuition by realizing patterns, hypothesizing, testing, and reaching conclusions (Aydemir, 2020). There are many different mathematical aspects to the spirograph including application of the least common multiple, trigonometry, geometry, and modular arithmetic. Many of these concepts build off of the Utah common core standards for middle school and high school students.
Background
To understand the math behind spirographs, it is essential to first look at the history behind them. It hasn't been determined who exactly came up with the idea of the spirograph, but there are many different people who had influences on its invention.
One of these people was a Greek architect and engineer named Peter Hubert Desvignes. In 1827 he invented a device called a "speiragrah" that was created to produce spiral drawings and used to prevent forgeries on banknotes (Evans, 2021).

Another person who had an influence on the spirograph invention was Bruno Abakanowicz, a mathematician who invented a spirograph between 1881 and 1900 that was used by engineers to calculate an area that was delimited by curves (Evans, 2021). The spirograph toy was first introduced in 1907 with the idea of a Wondergraph. This toy was made of wood and a contraption that helped the pen spin around and create symmetrical drawings.

While there are many historical inventions of a spirograph like contraption, the spirograph toy that is known today was an invention of Denys Fisher in 1962. It was originally developed as a drafting tool that was created by meccano pieces, but because of influence from friends and family he marketed it as a toy in the early 60s (Coopee, 2023). Since then, many different spirograph applets have been created and they have become widely available.

Explanation of Mathematics
As previously mentioned, there are many different mathematical aspects of the spirograph. One of the main ones is the application of trigonometric concepts. The trigonometric relationships behind spirographs is an extension of trigonometry learned in secondary education. Spirographs can be described mathematically by finding their parametric equations. Consider the following figure by Juergen Koeller.

In this figure, R represents the radius of the big circle and is a fixed value. P also represents a fixed value that has distance a from the center M of the small circle. P can be any of the holes on the small rotating circle. Also, r represents the radius of the small circle. When the small circle is being rotated, we follow the point P. The following parametric equations represent the movement of the point with x and y being the coordinates of point P depending on the angle t. No matter where P is, R and r always stay constant (Koeller, 2000).

Another mathematical concept behind the spirograph is geometry. There are different forms of geometrical shapes made by spirographs and these are influenced by the location of the pen hole. First, if the pen hole is at the center of the small circle, the curve made will simply be a circle centered at the center of the big circle. If the pen hole is at the edge of the small circle it will create a shape with a set of curves that bounce off the edges of the big circle and create pointed curves. This shape is called a hypocycloid (Steckles, 2022). The following figure shows an example of these.

If the pen hole isn’t in the center or on the edge, then it is dependent on r/R and P. This then creates a type of shape called hypotrochoids that may be various shapes. Some may be similar to a circle and some similar to a hypocycloid. Here is an example of this shape.

There are also some formulas that can determine how many petals (the outside points of the spiral) a shape has and how many rotations are needed to close a shape based on the number of teeth of the inside and outside gears. Least common multiple and modular arithmetic are both mathematical concepts that are used in these formulas. These ideas build off of the idea of least common multiple that is learned in eighth grade and arithmetic with polynomials which is learned in Secondary Math III. The number of petals N can be modeled by the formula N=LCM(R,W)/R where R is the number of teeth on the rotating disc and W is the number of teeth on the wheel (Rusenko, et al.). The number of rotations can be modeled by N= Z_x,ord (y)(y/x) where x is the number of teeth on the wheel and y is the number of teeth on the rotating disc (Brown, 2008).
This applet helps students explore the parametric equations of spirographs and how different parts of the equations create hypotrochoids and hypocycloids.
Applications/Significance
Spirographs have many applications, but with today’s technology a lot of them are outdated. Today we have computers that can generate any curves and allow for better exploration (Shell-Gellasch, 2018). However, in the late 19th and early 20th centuries spirographs were used for educational purposes and were great teaching devices. The mathematical concepts behind spirographs can also be used in engineering and art and design. Also, spirographs and spirograph applets can be used in secondary schools to explore these concepts and introduce students to different math related technologies.
References
Aydemir, E. (2021, July 26). Spirograph. Math Fan. https://www.mathcuriosity.com/post/spirograph
Brown, D. (2008, November 13). Spirographs: An application of Modular Arithmetic. The Math 152 Weblog. https://math152.wordpress.com/2008/11/13/spirographs-an-application-of-modular-arithmetic/
Coopee, T. (2023, September 14). Spirograph from Kenner (1967). Toy Tales. https://toytales.ca/spirograph-from-kenner-1967/
Evans, R. (2021). The history of Spirograph. Spirograph Girl. https://www.spirographgirl.com/blog/the-history-of-spirograph
Kaveney, W. (2004b). The Marvelous Wondergraph. CONTENTdm. https://www.digitalindy.org/digital/collection/tcm/id/787/
Koeller, J. (2000). Spirograph. https://www.mathematische-basteleien.de/spirographs.htm#:~:text=The%20trigonometric%20formulas%20guarantee%20periodical,the%20periodicity%20
of%20the%20drawings.&text=If%20you%20use%20a%20program,get%20the%20so%2Dcalled%20hypocycloids.&text=T
he%20parameter%20a%20is%20different%20for%20each%20picture.
Rusenko, D., Veltri, D., & Fanini, C. (n.d.). The math of spirographs. Mathematics Teaching and Learning. http://mathadinfinitum.weebly.com/the-math-of-spirographs.html
Shell-Gellasch, A. (2017, March 17). The Spirograph and kinematic models: Making math touchable (and pretty). National Museum of American History. https://americanhistory.si.edu/blog/2014/03/the-spirograph-and-kinematic-models-making-math-touchable-and-pretty.html
Steckles, K. (2022, December 21). The Mathematics of Spirograph. The Aperiodical. https://aperiodical.com/2021/12/the-mathematics-of-spirograph/
To understand the math behind spirographs, it is essential to first look at the history behind them. It hasn't been determined who exactly came up with the idea of the spirograph, but there are many different people who had influences on its invention. One of these people was a Greek architect and engineer named Peter Hubert Desvignes. In 1827 he invented a device called a "speiragrah" that was created to produce spiral drawings and used to prevent forgeries on banknotes (Evans, 2021).



Explanation of Mathematics
As previously mentioned, there are many different mathematical aspects of the spirograph. One of the main ones is the application of trigonometric concepts. The trigonometric relationships behind spirographs is an extension of trigonometry learned in secondary education. Spirographs can be described mathematically by finding their parametric equations. Consider the following figure by Juergen Koeller.

In this figure, R represents the radius of the big circle and is a fixed value. P also represents a fixed value that has distance a from the center M of the small circle. P can be any of the holes on the small rotating circle. Also, r represents the radius of the small circle. When the small circle is being rotated, we follow the point P. The following parametric equations represent the movement of the point with x and y being the coordinates of point P depending on the angle t. No matter where P is, R and r always stay constant (Koeller, 2000).

Another mathematical concept behind the spirograph is geometry. There are different forms of geometrical shapes made by spirographs and these are influenced by the location of the pen hole. First, if the pen hole is at the center of the small circle, the curve made will simply be a circle centered at the center of the big circle. If the pen hole is at the edge of the small circle it will create a shape with a set of curves that bounce off the edges of the big circle and create pointed curves. This shape is called a hypocycloid (Steckles, 2022). The following figure shows an example of these.

If the pen hole isn’t in the center or on the edge, then it is dependent on r/R and P. This then creates a type of shape called hypotrochoids that may be various shapes. Some may be similar to a circle and some similar to a hypocycloid. Here is an example of this shape.

There are also some formulas that can determine how many petals (the outside points of the spiral) a shape has and how many rotations are needed to close a shape based on the number of teeth of the inside and outside gears. Least common multiple and modular arithmetic are both mathematical concepts that are used in these formulas. These ideas build off of the idea of least common multiple that is learned in eighth grade and arithmetic with polynomials which is learned in Secondary Math III. The number of petals N can be modeled by the formula N=LCM(R,W)/R where R is the number of teeth on the rotating disc and W is the number of teeth on the wheel (Rusenko, et al.). The number of rotations can be modeled by N= Z_x,ord (y)(y/x) where x is the number of teeth on the wheel and y is the number of teeth on the rotating disc (Brown, 2008).
This applet helps students explore the parametric equations of spirographs and how different parts of the equations create hypotrochoids and hypocycloids.
Applications/Significance
Spirographs have many applications, but with today’s technology a lot of them are outdated. Today we have computers that can generate any curves and allow for better exploration (Shell-Gellasch, 2018). However, in the late 19th and early 20th centuries spirographs were used for educational purposes and were great teaching devices. The mathematical concepts behind spirographs can also be used in engineering and art and design. Also, spirographs and spirograph applets can be used in secondary schools to explore these concepts and introduce students to different math related technologies.
References
Aydemir, E. (2021, July 26). Spirograph. Math Fan. https://www.mathcuriosity.com/post/spirograph
Brown, D. (2008, November 13). Spirographs: An application of Modular Arithmetic. The Math 152 Weblog. https://math152.wordpress.com/2008/11/13/spirographs-an-application-of-modular-arithmetic/
Coopee, T. (2023, September 14). Spirograph from Kenner (1967). Toy Tales. https://toytales.ca/spirograph-from-kenner-1967/
Evans, R. (2021). The history of Spirograph. Spirograph Girl. https://www.spirographgirl.com/blog/the-history-of-spirograph
Kaveney, W. (2004b). The Marvelous Wondergraph. CONTENTdm. https://www.digitalindy.org/digital/collection/tcm/id/787/
Koeller, J. (2000). Spirograph. https://www.mathematische-basteleien.de/spirographs.htm#:~:text=The%20trigonometric%20formulas%20guarantee%20periodical,the%20periodicity%20
of%20the%20drawings.&text=If%20you%20use%20a%20program,get%20the%20so%2Dcalled%20hypocycloids.&text=T
he%20parameter%20a%20is%20different%20for%20each%20picture.
Rusenko, D., Veltri, D., & Fanini, C. (n.d.). The math of spirographs. Mathematics Teaching and Learning. http://mathadinfinitum.weebly.com/the-math-of-spirographs.html
Shell-Gellasch, A. (2017, March 17). The Spirograph and kinematic models: Making math touchable (and pretty). National Museum of American History. https://americanhistory.si.edu/blog/2014/03/the-spirograph-and-kinematic-models-making-math-touchable-and-pretty.html
Steckles, K. (2022, December 21). The Mathematics of Spirograph. The Aperiodical. https://aperiodical.com/2021/12/the-mathematics-of-spirograph/




Applications/Significance
Spirographs have many applications, but with today’s technology a lot of them are outdated. Today we have computers that can generate any curves and allow for better exploration (Shell-Gellasch, 2018). However, in the late 19th and early 20th centuries spirographs were used for educational purposes and were great teaching devices. The mathematical concepts behind spirographs can also be used in engineering and art and design. Also, spirographs and spirograph applets can be used in secondary schools to explore these concepts and introduce students to different math related technologies.
References
Aydemir, E. (2021, July 26). Spirograph. Math Fan. https://www.mathcuriosity.com/post/spirograph
Brown, D. (2008, November 13). Spirographs: An application of Modular Arithmetic. The Math 152 Weblog. https://math152.wordpress.com/2008/11/13/spirographs-an-application-of-modular-arithmetic/
Coopee, T. (2023, September 14). Spirograph from Kenner (1967). Toy Tales. https://toytales.ca/spirograph-from-kenner-1967/
Evans, R. (2021). The history of Spirograph. Spirograph Girl. https://www.spirographgirl.com/blog/the-history-of-spirograph
Kaveney, W. (2004b). The Marvelous Wondergraph. CONTENTdm. https://www.digitalindy.org/digital/collection/tcm/id/787/
Koeller, J. (2000). Spirograph. https://www.mathematische-basteleien.de/spirographs.htm#:~:text=The%20trigonometric%20formulas%20guarantee%20periodical,the%20periodicity%20
of%20the%20drawings.&text=If%20you%20use%20a%20program,get%20the%20so%2Dcalled%20hypocycloids.&text=T
he%20parameter%20a%20is%20different%20for%20each%20picture.
Rusenko, D., Veltri, D., & Fanini, C. (n.d.). The math of spirographs. Mathematics Teaching and Learning. http://mathadinfinitum.weebly.com/the-math-of-spirographs.html
Shell-Gellasch, A. (2017, March 17). The Spirograph and kinematic models: Making math touchable (and pretty). National Museum of American History. https://americanhistory.si.edu/blog/2014/03/the-spirograph-and-kinematic-models-making-math-touchable-and-pretty.html
Steckles, K. (2022, December 21). The Mathematics of Spirograph. The Aperiodical. https://aperiodical.com/2021/12/the-mathematics-of-spirograph/
References
Aydemir, E. (2021, July 26). Spirograph. Math Fan. https://www.mathcuriosity.com/post/spirograph
Brown, D. (2008, November 13). Spirographs: An application of Modular Arithmetic. The Math 152 Weblog. https://math152.wordpress.com/2008/11/13/spirographs-an-application-of-modular-arithmetic/
Coopee, T. (2023, September 14). Spirograph from Kenner (1967). Toy Tales. https://toytales.ca/spirograph-from-kenner-1967/
Evans, R. (2021). The history of Spirograph. Spirograph Girl. https://www.spirographgirl.com/blog/the-history-of-spirograph
Kaveney, W. (2004b). The Marvelous Wondergraph. CONTENTdm. https://www.digitalindy.org/digital/collection/tcm/id/787/
Koeller, J. (2000). Spirograph. https://www.mathematische-basteleien.de/spirographs.htm#:~:text=The%20trigonometric%20formulas%20guarantee%20periodical,the%20periodicity%20
of%20the%20drawings.&text=If%20you%20use%20a%20program,get%20the%20so%2Dcalled%20hypocycloids.&text=T
he%20parameter%20a%20is%20different%20for%20each%20picture.
Rusenko, D., Veltri, D., & Fanini, C. (n.d.). The math of spirographs. Mathematics Teaching and Learning. http://mathadinfinitum.weebly.com/the-math-of-spirographs.html
Shell-Gellasch, A. (2017, March 17). The Spirograph and kinematic models: Making math touchable (and pretty). National Museum of American History. https://americanhistory.si.edu/blog/2014/03/the-spirograph-and-kinematic-models-making-math-touchable-and-pretty.html
Steckles, K. (2022, December 21). The Mathematics of Spirograph. The Aperiodical. https://aperiodical.com/2021/12/the-mathematics-of-spirograph/
Aydemir, E. (2021, July 26). Spirograph. Math Fan. https://www.mathcuriosity.com/post/spirograph
Brown, D. (2008, November 13). Spirographs: An application of Modular Arithmetic. The Math 152 Weblog. https://math152.wordpress.com/2008/11/13/spirographs-an-application-of-modular-arithmetic/
Coopee, T. (2023, September 14). Spirograph from Kenner (1967). Toy Tales. https://toytales.ca/spirograph-from-kenner-1967/
Evans, R. (2021). The history of Spirograph. Spirograph Girl. https://www.spirographgirl.com/blog/the-history-of-spirograph
Kaveney, W. (2004b). The Marvelous Wondergraph. CONTENTdm. https://www.digitalindy.org/digital/collection/tcm/id/787/
Koeller, J. (2000). Spirograph. https://www.mathematische-basteleien.de/spirographs.htm#:~:text=The%20trigonometric%20formulas%20guarantee%20periodical,the%20periodicity%20 of%20the%20drawings.&text=If%20you%20use%20a%20program,get%20the%20so%2Dcalled%20hypocycloids.&text=T he%20parameter%20a%20is%20different%20for%20each%20picture.
Rusenko, D., Veltri, D., & Fanini, C. (n.d.). The math of spirographs. Mathematics Teaching and Learning. http://mathadinfinitum.weebly.com/the-math-of-spirographs.html
Shell-Gellasch, A. (2017, March 17). The Spirograph and kinematic models: Making math touchable (and pretty). National Museum of American History. https://americanhistory.si.edu/blog/2014/03/the-spirograph-and-kinematic-models-making-math-touchable-and-pretty.html
Steckles, K. (2022, December 21). The Mathematics of Spirograph. The Aperiodical. https://aperiodical.com/2021/12/the-mathematics-of-spirograph/