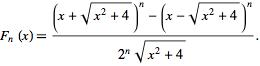The Mathematics of the Fibonacci Sequence

The Fibonacci Sequence can be found with the equation below:
F_n=F_n-1+F_n-2
Each Fibonacci number is the addition of the two previous numbers: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 ...

Fibonacci numbers can also be found by the formula
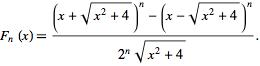
F_n(x)=((x+sqrt(x^2+4))^n-(x-sqrt(x^2+4))^n)/(2^nsqrt(x^2+4))

F_n(x)=((x+sqrt(x^2+4))^n-(x-sqrt(x^2+4))^n)/(2^nsqrt(x^2+4))

where F_n (1) equals a Fibonacci number.
The resulting polynomials are known as Fibonacci Polynomials (Weisstein). You can explore the Fibonacci Polynomials in the applet below or visit this website.

How to find out if a number is a Fibonacci Number

Have you ever wondered if a number is in the Fibonacci sequence? A proof by Ira Gessel at Harvard University shows that a positive integer n is a Fibonacci number if and only if 5n²+4 or 5n²-4 is a perfect square. You can view this proof and others in this pdf.

Fibonacci Pattern

There are also several patterns and ratios inside the Fibonacci sequence. One such pattern is shown by squaring the Fibonacci numbers. The addition of two squared Fibonacci numbers will equal a Fibonacci number.
1²+1²=2
1²+2²=5
2²+3²=13
3²+5²=34
and so on.
If you add up several of the squared Fibonacci numbers then you will receive multiples of Fibonacci numbers: 1²+1²+2²=6=2*3
1²+1²+2²+3²=15=3*5
1²+1²+2²+3²+5²=40=5*8
1²+1²+2²+3²+5²+6²=104=8*13

This can be explained visually with the Fibonacci rectangle.

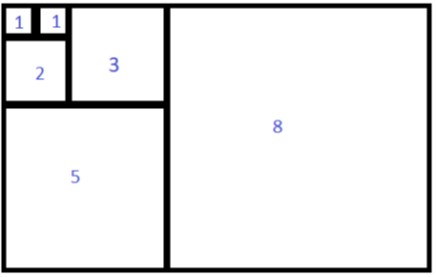
If you add up the areas of the individuals squares, 1²+1²+2²+3²+5², then it will equal the whole area of the rectangle which is also equal to the width, 13, multiplied by the height, 8 (Debnath, 2011).

Top