Methods for Multiplying Polynomials
Now that we have reviewed what a polynomial is, we are going to focus on how to multiply them together. We'll start with monomials multiplying monomials.

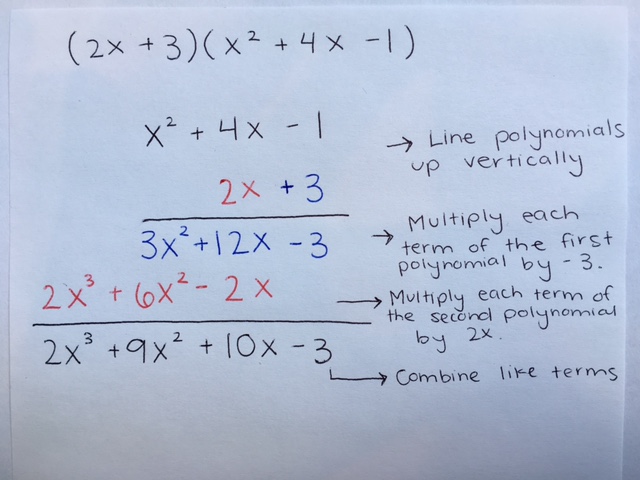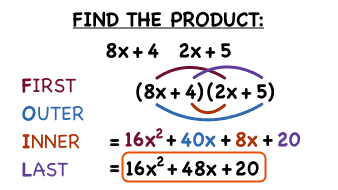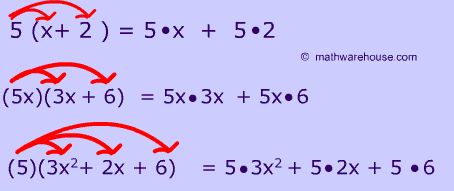
(3)(2x)= 6x	We multiply like terms
(3x)(-4x²)= -12x³	How to multiply variables with exponents
(3xy)(5zy)= 15xy²z	How to multiply with multiple variables

Now, when multiplying monomials into binomials and trinomials, we use the distributive property, as shown below.


Multiplying binomials and trinomials take a little more work. We all learn differently, so explore the following methods to see which one works the best for you. There will be four methods shown, 1) The Table Method, 2) The Vertical Method, 3) The F-O-I-L Method, and 4) The Geometric Method



1) The Table Method
Suppose we needed to simplify (x-3)(4x-5). First, set up a table. Put each term from the first binomial above a separate box in the first row(as shown). Then, put a term from the second binomial beside separate boxes in the first column (as shown). Multiply the terms from the rows and columns together to complete your table. Then combine like terms.


Watch an example of using the table method to multiply binomials.
Here is another look at the table method, this time using binomials and trinomials!


2) The Vertical Method
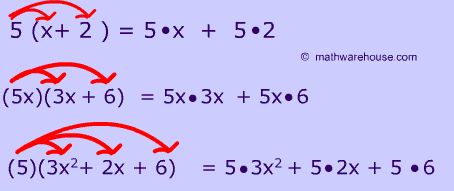
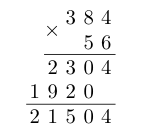Remember this? Multiplying large numbers if often demonstrated by using the vertical method. We can use the same set-up to multiply polynomials.

As this figure shows, it follows the same pattern that multiplying large numbers follows. Make sure to multiply the sign through with the polynomials, and line up the like terms in vertical columns. This method can be used for multiplying monomials and trinomials as well.


3) The F-O-I-L Method
This method may be the most used and most well known. FOIL is an acronym which stands for First, Outside, Inside, Last. This was used as a way to help you remember how to multiply two binomials together. Remember, this is not a technical mathematic term, just a way to help you rememer how to multiply binomials. Another warning with the F-O-I-L method: It ONLY works for multiplying two binomials. With that all said, let's get started!
A generic case of "foiling" would look like this:
We multiply the first terms in both polynomials (a*c).
Then we multiply the ourtermost terms (a*d).
The inside terms are the middle most terms (b*c).
Finish by multiplying the last terms in each polynomial (b*d).
Now just combine like terms!
Here is an example with specific numbers:

Remember that F-O-I-L will only work for multiplying two binomials.

Here's a little practice on multiplying polynomials using the first three methods.


4) The Geometric Method
Now, for you visual, kinesthetic learners!
When we multiply polynomials together, we can think of it as finding the area of a rectangle. Engage in the following activity to visualize what you are doing.

A similar way to visualize multiplying polynomials is by algebra tiles.
To build your own rectangle using lengths x, y, and 1, check out the algebra tiles found at http://technology.cpm.org/general/tiles/


1. Click on "Backgrounds" and add the Cornerpiece.
2. Click on "Algebra Tiles"
3. Create a visual representation of (2x+y)(y+3) by lining the appropriate algebra tiles to the left and under axis.
Double click to change direction of tiles.
4. Add the appropriate squares and rectangles. Add the area of all rectangles.
You should have 2 xy rectangles, 6 x rectangles, 1 y² rectangle, and 3 y rectangles.
So, (2x+y)(y+3)= 2xy+6x+y² + 3y.
5. Now, click and hold one of the y pieces to turn it negative.
6. How does that affect your graph? How will it affect your answer? Compare with your neighbor.

Back to top