Sextics
It is known that there are not general equations for
polynomials of degree 5 or higher (see proof here),
which is why Descartes’ method to solving sextics
(polynomials of degree 6) is so intriguing to me.
Descartes’ Rule of Signs
Early on in The
Geometry, Descartes explained his Rule of Signs. We still use this rule and method today. It helps us get an idea how many of each type
of roots a polynomial has. It gives a
range how many of each type of root a polynomial has (that is positive real,
negative real, and complex). We use a
table to organize this:
|
Positive Real |
Negative Real |
Complex |
|
|
|
|
|
|
|
|
To find the
upper bound of how many positive real roots there are, we are going to look at
the polynomial given to us in the form ![]() where
where ![]() is a nonzero constant term. Count the number of sign changes between each
term. This number goes in the positive
real column and is the maximum number of positive real roots there will
be.
is a nonzero constant term. Count the number of sign changes between each
term. This number goes in the positive
real column and is the maximum number of positive real roots there will
be.
To find the
upper bound of how many negative real roots there are, we are going to look at
the polynomial ![]() Simplify, and count the number of sign changes between each term. This number goes in the negative real column
and is the maximum number of negative real roots
there will be.
Simplify, and count the number of sign changes between each term. This number goes in the negative real column
and is the maximum number of negative real roots
there will be.
We will use
the Fundamental Theorem of Algebra to fill in the complex column of our
table. The Fundamental Theorem of
Algebra states that a polynomial of degree n will have n solutions. So if you have a polynomial of degree 6, and
you wrote 2 in the positive column, and 2 in the negative column, you will
write 2 in the complex column because there will be a total of 6 roots. You now
have the maximum number of complex roots.
To fill in
the rest of the table, (to write all possibilities of solutions you could get),
we will go down 2 in both the positive real column and the negative real column
(if it permits; we could not get a negative amount of zeros). After we do this, we will adjust the complex
column accordingly (so that way we will still have 6 total roots). We need to remember to list all combinations
of possibilities.
You can see
examples of Descartes’ Rule of Signs here.
I have reminded you of Descartes’ Rule of Signs because the first step to
solving the roots of sextic polynomials (polynomials
of degree 6) is to convert the sextic polynomial into
a polynomial with all positive roots.
You do this by plugging in ![]() into
into ![]() in the sixth degree polynomial, where c is
larger than the amount of all the polynomial’s real negative roots. Remember we can find the maximum number of a
polynomial’s real negative roots by using Descartes’ rule of signs by counting
the number of sign changes in the polynomial
in the sixth degree polynomial, where c is
larger than the amount of all the polynomial’s real negative roots. Remember we can find the maximum number of a
polynomial’s real negative roots by using Descartes’ rule of signs by counting
the number of sign changes in the polynomial ![]() (see above). So we will chose a
value for c that is larger than the amount of all the polynomial’s real
negative roots and plug in
(see above). So we will chose a
value for c that is larger than the amount of all the polynomial’s real
negative roots and plug in ![]() into our polynomial. (Rubinstein, 6)
into our polynomial. (Rubinstein, 6)
Now we have a sextic polynomial, in
the form ![]() , where
, where ![]() is a negative coefficient,
is a negative coefficient, ![]() is a positive coefficient,
is a positive coefficient, ![]() is a negative coefficient,
is a negative coefficient, ![]() is a positive coefficient,
is a positive coefficient, ![]() is a negative coefficient, and
is a negative coefficient, and ![]() is a positive constant, and
is a positive constant, and ![]() (which is satisfied when we substituted
(which is satisfied when we substituted ![]() in for
in for ![]() .
(Rubinstein, 6)
.
(Rubinstein, 6)
Let ![]() .
Graph the Cartesian parabola:
.
Graph the Cartesian parabola: ![]() , and the circle
, and the circle ![]() where
where ![]() ,
, ![]() and
and ![]() .
The intersections of the Cartesian parabola and the circle will be the
real roots of the converted sextic polynomial. (Rubinstein, 6)
.
The intersections of the Cartesian parabola and the circle will be the
real roots of the converted sextic polynomial. (Rubinstein, 6)
But what do the roots of the ‘converted’ sextic
tell us about the original sextic polynomial?
This is just like the last step of Descartes’ method for solving for the roots
of quartic polynomials. We plug in our
root in for x in (x-c). This will give us the actual root of the
polynomial. (Rubinstein, 6)
See it in action!
There are some awesome applets that show this in play on this
site:
Why does it work?
I will show why the intersection of this circle and this
Cartesian parabola make up the real roots of the converted sextic
polynomial.
First, start with the generic equations of the Cartesian
parabola and the circle:
![]()
![]()
(Rubinstein, 9)
Plug in ![]() for
for ![]() :
:
![]()
(Rubinstein, 9)
Simplify:
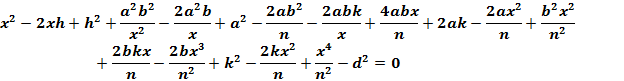
(Rubinstein, 9)
Multiply both sides of the equation by ![]() :
:
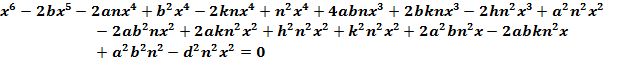
(Rubinstein, 9)
Factor:
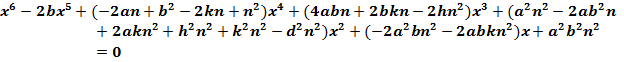
(Rubinstein, 9)
Use the method of equating coefficients with the general form
of a sextic polynomial:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(Rubinstein, 9)
We now have six equations and six unknowns, so we can solve
for a, b, d, n, h, and k.
To solve for b,
From equation (2), solve for b:
![]()
(Rubinstein, 9)
To solve for a,
From equation (7):
![]()
Plug in ![]() :
:
![]()
(Rubinstein, 9)
To solve for n,
From equation (3), solve for n:
![]()
Use what we know from equation (7):
![]()
Substitute into equation (6):
![]()
Factor out ![]()
![]()
Divide ![]() on both sides:
on both sides:
![]()
Plug ![]() into
into ![]() :
:
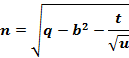
Plug in ![]() :
:
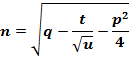
(Rubinstein, 9)
To solve for h,
From equation (4), solve for ![]() :
:
![]()
Plug in ![]() and
and ![]() :
:
![]()
Rewrite the third term:
![]()
Combine the third and fourth term:
![]()
Plug in ![]() and
and ![]() :
:
![]()
Factor out a ![]() from the numerator of the third term:
from the numerator of the third term:
![]()
Plug in again ![]() and equation (6)
and equation (6) ![]()
![]()
(Rubinstein, 9)
To solve for k,
Use equation (6) to solve for k:
![]()
Simplify:
![]()
Plug in ![]() and
and ![]() :
:
![]()
(Rubinstein, 9)
To solve for d,
Use equation (5) to solve for ![]() :
:
![]()
Simplify:
![]()
Simplify:
![]()
Plug in ![]() :
:
![]()
Plug in ![]() :
:
![]()
Square root both sides:
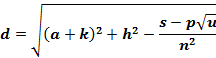
(Rubinstein, 9)
Click here for a challenge.