Euclid's Elements Book 1
Proposition 1: Make an Equilateral triangle with two similar circles
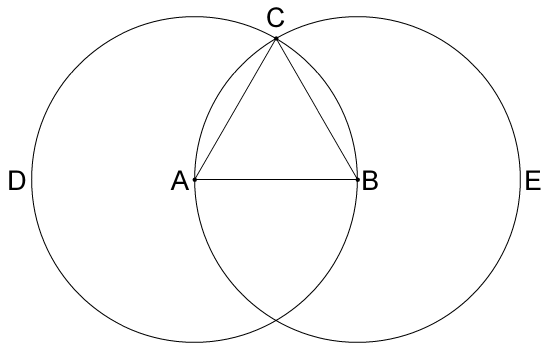
Constract a circle with the center point A. Then pick a point on the circle and name it B. Make a new circle with B as the center point and AB as the radius. Now create a new segment AC and another new segment BC. The first circle we see that segement AB is congruent to AC. The second circle we see that AB is congruent BC. Therefore AB is congruent to AC and BC. Making an equalilateral triangle Which is the very thing it was required to do.
Proposition 2: Place a straight line equal to a given straight-line at a given point.
In other words you have a segment AB and a point C. Create a new segment the same length of segment AB starting with the point C.
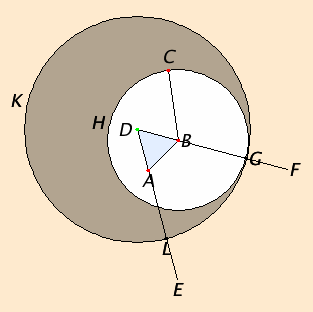
Given the circle GLK whose center is D. Given the circle HCG whose center is B. Make an equilateral triangle with D, B, and construct a point A. Now draw segments AL, BC, and BG. We know DG is equal length to DL since the point D is the center of circle KGL. We also find that BG is equal to BC. This now makes the length DBC equal to DAL. Since DB is equal to DA we know that AL is equal to CB. Which is the very thing it was required to do.
The above picture is the drawing with Euclids text for a visual.
Proposition 3
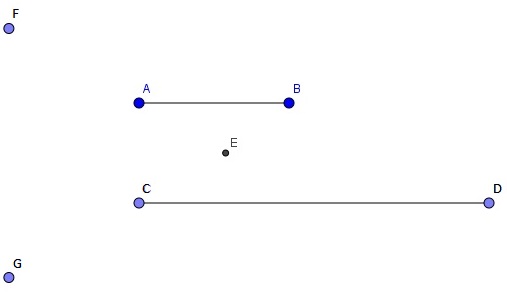
Using the picture above.
When you have two segments of different lengths then we can make a point on the longer segment to make a new segment that is equal to the shorter segment.
We have the two segments AB and CD. So we want to have the exact segment length AB congruent to Point C and some point on the segment CD.
We start by making A the center of a circle that intersects at point C. Then we use point C as the center of a circle with radius to point A. Using Proposition two we know this makes an equilateral triangle. Triangle ACE.
Using the point E as the center point we make a new circle and the radius is the length EB. Then draw a segment from E to the new circle through A to make a new point F. Then using E and EF as the radius construct a new circle. Then draw a new segment from F to the new circle through the point C.
Then draw a circle with C as the center and CG as the radius. Where the new circle intersects segment CD make a new point. We now know AB is congruent to AF;AF is congruent to CG; Then AB is congruent to GC. Since GC is congruent to CH; AB is Congruent to CH. Therefore AB is projected on CD as CH. Which is the very thing is was required to do.
Proposition 4
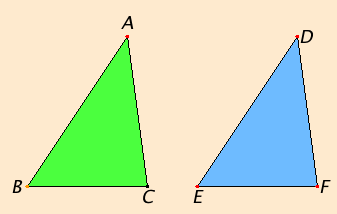
Two triangles that have two sides equal to two sides and equal angles. Then those two triangles base will also be equal to each other. Also the remaining angles will be congruent to each other.
Proposition 5
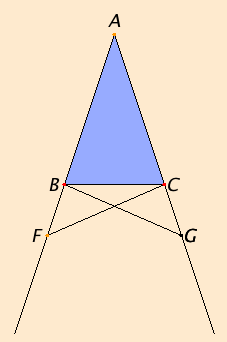
Proposition 6
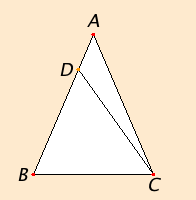
Proposition 7
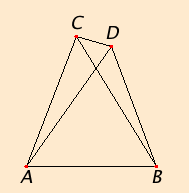
Proposition 8
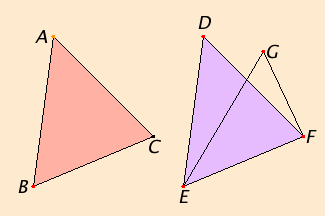
Proposition 9
Proposition 10
Top









