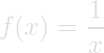
This trumpet shape will have infinite surface area and a finite volume. The paradox has become known as the painter's paradox
"since the Horn has finite volume but infinite surface area, it seems that it could be filled with a finite quantity of paint,
and yet the paint would not be sufficient to coat its surface - an apparent paradox"
This paradox is sometimes referred to Gabriel's Trumpet name after the arch angle in the bible.
Toricelli proved his discovery using
Calvalieri's method of indivisibiles a method used before the invention of calculus.
Today we have the advantage of using calculus to calculate the surface area and volume of this curve. We will begin by finding the volume.
Volume
The (V) volume can be found using simple integration, using the disk method.
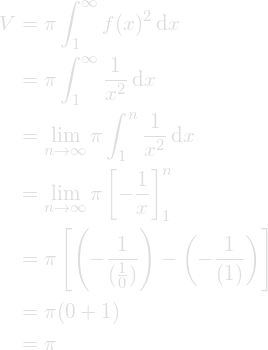
The volume of the trumpet will never exceed pi as n approaches infinity. This shows us the volume has a finite limit and therefore must also be finite.
Surface Area
To find the (SA) surface area we will use need to use partial differentiation and integration.
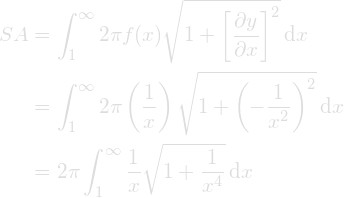
At this point we can use a little trick to simplify this integral and make it a whole lot easier. All we need to do is use the fact that the following is true.
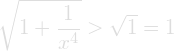
Now we substitute this trick into the original equation and see that the following is also true.
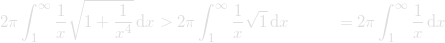
Using this method trick we simplify our equation and can now more easily solve the integral and see how it converges.
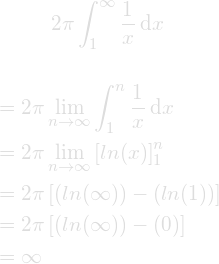
The results of this integral shows the surface area of Torricelli's Trumpet is infinite. As n approaches infinity the length of the horn becomes infinite. Rotating around the x axis maintains the infinity properties while producing a horn shape.
We have just shown that Torricelli's Trumpet has an infinite surface area with a finite volume. Therefore, paradoxically, we could fill the
trumpet with a finite amount of paint yet never have enough paint to paint the surface.

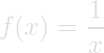

Volume
The (V) volume can be found using simple integration, using the disk method.
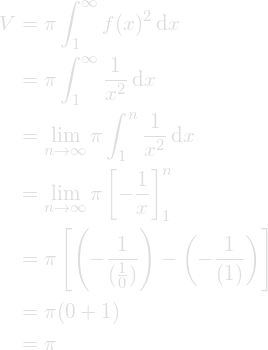
The volume of the trumpet will never exceed pi as n approaches infinity. This shows us the volume has a finite limit and therefore must also be finite.
Surface Area
To find the (SA) surface area we will use need to use partial differentiation and integration.
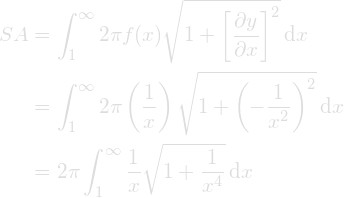
At this point we can use a little trick to simplify this integral and make it a whole lot easier. All we need to do is use the fact that the following is true.
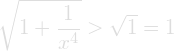
Now we substitute this trick into the original equation and see that the following is also true.
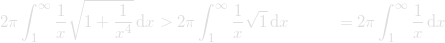
Using this method trick we simplify our equation and can now more easily solve the integral and see how it converges.
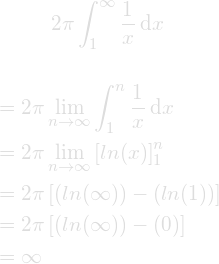
The results of this integral shows the surface area of Torricelli's Trumpet is infinite. As n approaches infinity the length of the horn becomes infinite. Rotating around the x axis maintains the infinity properties while producing a horn shape.
We have just shown that Torricelli's Trumpet has an infinite surface area with a finite volume. Therefore, paradoxically, we could fill the
trumpet with a finite amount of paint yet never have enough paint to paint the surface.

The (V) volume can be found using simple integration, using the disk method.
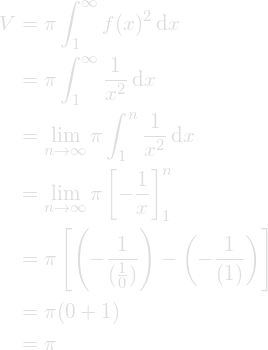
The volume of the trumpet will never exceed pi as n approaches infinity. This shows us the volume has a finite limit and therefore must also be finite.
Surface Area
To find the (SA) surface area we will use need to use partial differentiation and integration.
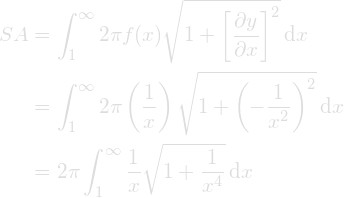
At this point we can use a little trick to simplify this integral and make it a whole lot easier. All we need to do is use the fact that the following is true.
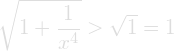
Now we substitute this trick into the original equation and see that the following is also true.
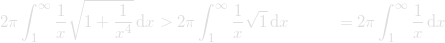
Using this method trick we simplify our equation and can now more easily solve the integral and see how it converges.
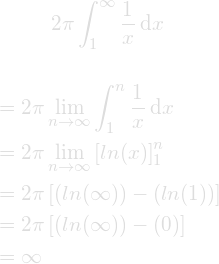
The results of this integral shows the surface area of Torricelli's Trumpet is infinite. As n approaches infinity the length of the horn becomes infinite. Rotating around the x axis maintains the infinity properties while producing a horn shape.
We have just shown that Torricelli's Trumpet has an infinite surface area with a finite volume. Therefore, paradoxically, we could fill the
trumpet with a finite amount of paint yet never have enough paint to paint the surface.

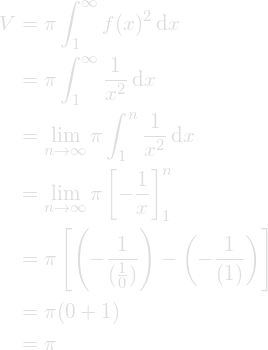
The volume of the trumpet will never exceed pi as n approaches infinity. This shows us the volume has a finite limit and therefore must also be finite.
Surface Area
To find the (SA) surface area we will use need to use partial differentiation and integration.
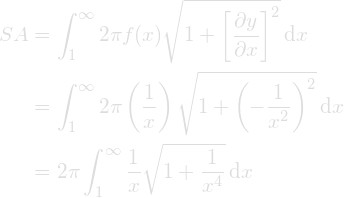
At this point we can use a little trick to simplify this integral and make it a whole lot easier. All we need to do is use the fact that the following is true.
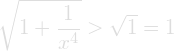
Now we substitute this trick into the original equation and see that the following is also true.
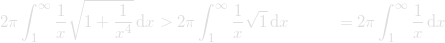
Using this method trick we simplify our equation and can now more easily solve the integral and see how it converges.
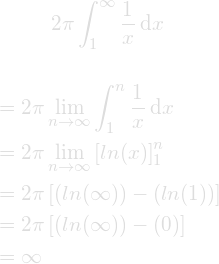
The results of this integral shows the surface area of Torricelli's Trumpet is infinite. As n approaches infinity the length of the horn becomes infinite. Rotating around the x axis maintains the infinity properties while producing a horn shape.
We have just shown that Torricelli's Trumpet has an infinite surface area with a finite volume. Therefore, paradoxically, we could fill the
trumpet with a finite amount of paint yet never have enough paint to paint the surface.

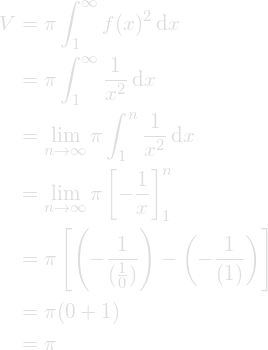
The volume of the trumpet will never exceed pi as n approaches infinity. This shows us the volume has a finite limit and therefore must also be finite.
Surface Area
To find the (SA) surface area we will use need to use partial differentiation and integration.
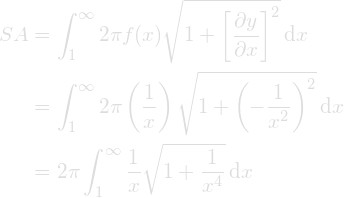
At this point we can use a little trick to simplify this integral and make it a whole lot easier. All we need to do is use the fact that the following is true.
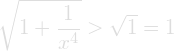
Now we substitute this trick into the original equation and see that the following is also true.
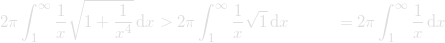
Using this method trick we simplify our equation and can now more easily solve the integral and see how it converges.
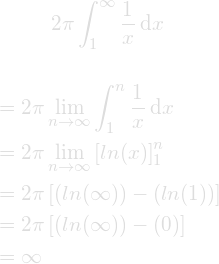
The results of this integral shows the surface area of Torricelli's Trumpet is infinite. As n approaches infinity the length of the horn becomes infinite. Rotating around the x axis maintains the infinity properties while producing a horn shape.
We have just shown that Torricelli's Trumpet has an infinite surface area with a finite volume. Therefore, paradoxically, we could fill the
trumpet with a finite amount of paint yet never have enough paint to paint the surface.

Surface Area
To find the (SA) surface area we will use need to use partial differentiation and integration.
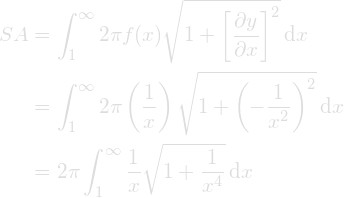
At this point we can use a little trick to simplify this integral and make it a whole lot easier. All we need to do is use the fact that the following is true.
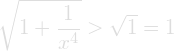
Now we substitute this trick into the original equation and see that the following is also true.
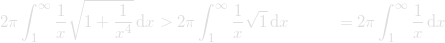
Using this method trick we simplify our equation and can now more easily solve the integral and see how it converges.
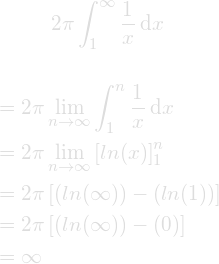
The results of this integral shows the surface area of Torricelli's Trumpet is infinite. As n approaches infinity the length of the horn becomes infinite. Rotating around the x axis maintains the infinity properties while producing a horn shape.
We have just shown that Torricelli's Trumpet has an infinite surface area with a finite volume. Therefore, paradoxically, we could fill the
trumpet with a finite amount of paint yet never have enough paint to paint the surface.

To find the (SA) surface area we will use need to use partial differentiation and integration.
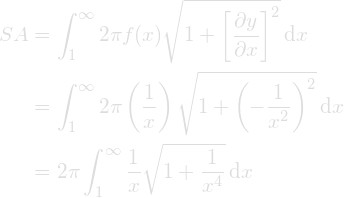
At this point we can use a little trick to simplify this integral and make it a whole lot easier. All we need to do is use the fact that the following is true.
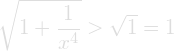
Now we substitute this trick into the original equation and see that the following is also true.
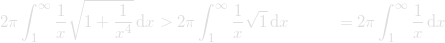
Using this method trick we simplify our equation and can now more easily solve the integral and see how it converges.
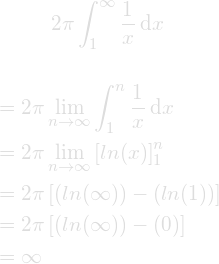
The results of this integral shows the surface area of Torricelli's Trumpet is infinite. As n approaches infinity the length of the horn becomes infinite. Rotating around the x axis maintains the infinity properties while producing a horn shape.
We have just shown that Torricelli's Trumpet has an infinite surface area with a finite volume. Therefore, paradoxically, we could fill the
trumpet with a finite amount of paint yet never have enough paint to paint the surface.

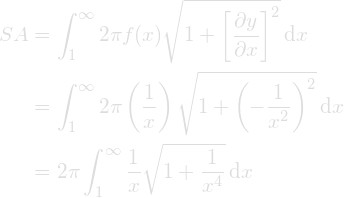
At this point we can use a little trick to simplify this integral and make it a whole lot easier. All we need to do is use the fact that the following is true.
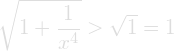
Now we substitute this trick into the original equation and see that the following is also true.
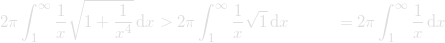
Using this method trick we simplify our equation and can now more easily solve the integral and see how it converges.
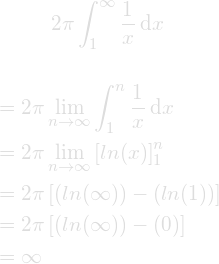
The results of this integral shows the surface area of Torricelli's Trumpet is infinite. As n approaches infinity the length of the horn becomes infinite. Rotating around the x axis maintains the infinity properties while producing a horn shape.
We have just shown that Torricelli's Trumpet has an infinite surface area with a finite volume. Therefore, paradoxically, we could fill the
trumpet with a finite amount of paint yet never have enough paint to paint the surface.

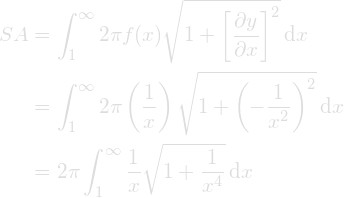
At this point we can use a little trick to simplify this integral and make it a whole lot easier. All we need to do is use the fact that the following is true.
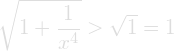
Now we substitute this trick into the original equation and see that the following is also true.
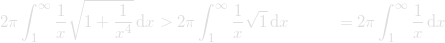
Using this method trick we simplify our equation and can now more easily solve the integral and see how it converges.
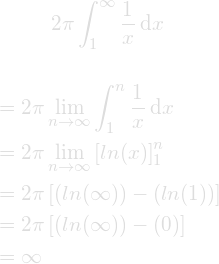
The results of this integral shows the surface area of Torricelli's Trumpet is infinite. As n approaches infinity the length of the horn becomes infinite. Rotating around the x axis maintains the infinity properties while producing a horn shape.
We have just shown that Torricelli's Trumpet has an infinite surface area with a finite volume. Therefore, paradoxically, we could fill the
trumpet with a finite amount of paint yet never have enough paint to paint the surface.

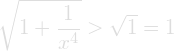
Now we substitute this trick into the original equation and see that the following is also true.
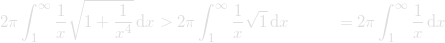
Using this method trick we simplify our equation and can now more easily solve the integral and see how it converges.
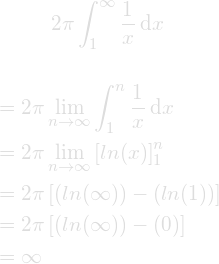
The results of this integral shows the surface area of Torricelli's Trumpet is infinite. As n approaches infinity the length of the horn becomes infinite. Rotating around the x axis maintains the infinity properties while producing a horn shape.
We have just shown that Torricelli's Trumpet has an infinite surface area with a finite volume. Therefore, paradoxically, we could fill the
trumpet with a finite amount of paint yet never have enough paint to paint the surface.

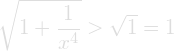
Now we substitute this trick into the original equation and see that the following is also true.
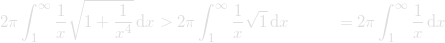
Using this method trick we simplify our equation and can now more easily solve the integral and see how it converges.
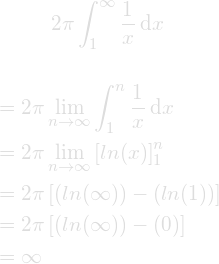
The results of this integral shows the surface area of Torricelli's Trumpet is infinite. As n approaches infinity the length of the horn becomes infinite. Rotating around the x axis maintains the infinity properties while producing a horn shape.
We have just shown that Torricelli's Trumpet has an infinite surface area with a finite volume. Therefore, paradoxically, we could fill the
trumpet with a finite amount of paint yet never have enough paint to paint the surface.

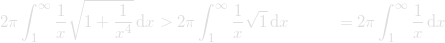
Using this method trick we simplify our equation and can now more easily solve the integral and see how it converges.
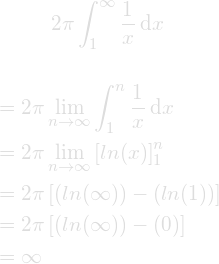
The results of this integral shows the surface area of Torricelli's Trumpet is infinite. As n approaches infinity the length of the horn becomes infinite. Rotating around the x axis maintains the infinity properties while producing a horn shape.
We have just shown that Torricelli's Trumpet has an infinite surface area with a finite volume. Therefore, paradoxically, we could fill the
trumpet with a finite amount of paint yet never have enough paint to paint the surface.

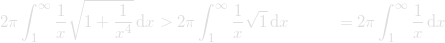
Using this method trick we simplify our equation and can now more easily solve the integral and see how it converges.
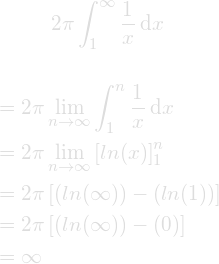
The results of this integral shows the surface area of Torricelli's Trumpet is infinite. As n approaches infinity the length of the horn becomes infinite. Rotating around the x axis maintains the infinity properties while producing a horn shape.
We have just shown that Torricelli's Trumpet has an infinite surface area with a finite volume. Therefore, paradoxically, we could fill the
trumpet with a finite amount of paint yet never have enough paint to paint the surface.

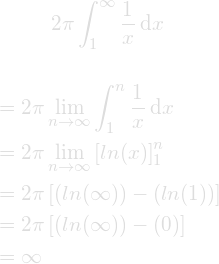
The results of this integral shows the surface area of Torricelli's Trumpet is infinite. As n approaches infinity the length of the horn becomes infinite. Rotating around the x axis maintains the infinity properties while producing a horn shape.
We have just shown that Torricelli's Trumpet has an infinite surface area with a finite volume. Therefore, paradoxically, we could fill the
trumpet with a finite amount of paint yet never have enough paint to paint the surface.

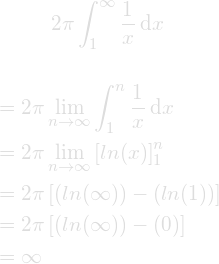
The results of this integral shows the surface area of Torricelli's Trumpet is infinite. As n approaches infinity the length of the horn becomes infinite. Rotating around the x axis maintains the infinity properties while producing a horn shape.
We have just shown that Torricelli's Trumpet has an infinite surface area with a finite volume. Therefore, paradoxically, we could fill the
trumpet with a finite amount of paint yet never have enough paint to paint the surface.

We have just shown that Torricelli's Trumpet has an infinite surface area with a finite volume. Therefore, paradoxically, we could fill the
trumpet with a finite amount of paint yet never have enough paint to paint the surface.

