History and Background
Anciently exponentials were used, however the terms and vocabulary that we are familiar with is not what they used a long time ago. An exponential function can loosely be defined as a geometric progression. This is not how I would have thought about an exponential function but does give an accurate representation. Lorenzo J. Curtis from the Department of Physics and Astronomy at the University of Toledo stated, "The exponential law is most concretely stated as a one-to-one correspondence between an arithmetic progression (formed by repeated successive addition of a quantity) such as 0, 1, 2, 3, 4, ... and a geometric progression (formed by repeated successive multiplication by a quantity) such as 1, 2, 4, 8, 16, ... or its reciprocal, the halving progression." This really helped me change my perspective about exponential functions or representations. Continuing Curtis states, "One of the most striking features of a geometric progression is its generation of large and small numbers. For example, 80 successive doublings of a 1-cm length exceeds the distance to the Andromeda nebula, and 80 successive halvings of 1 mole of material splits the last remaining molecule of the sample.

Many features of the geometric progression has been recognized long before even the time of Archimedes some of which had been recorded on Egyptian papyrus and Sumerian cuneiform tablets. The Ancient Egyptians were masters at geometric progression because their "entire system of basic arithmetic operations" were based on this concept. A famous problem from the Rhind papyrus suggested that the ancient Egyptians understood many of the basic properties of exponential functions. Problem number 79 is the famous puzzle of the seven housecats. The interpretation of the entries on the Rhind papyrus is this, "In a certain village there were 7 houses; each house had 7 cats; each cat caught 7 mice; each mouse (were it not for the cats) have eaten 7 ears of spelt; each ear of spelt produced 7 hekats (about half a peck) of grain at harvest. How many hekats of grain were saved by the presence of the cats and (unasked, but answered) how many heterogeneous elements are there in the sequence?" Neugebauer suggested a solution in 1926. The values in italics are his solution.
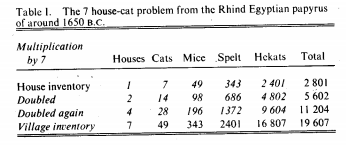
"The village inventory for each category is obtained by doubling the house inventory twice and adding the three entries. The village inventory for one item is numerically equal to the house inventory for the next item, so the process can be continued until the village inventory of saved grain (16,807 hekats) is obtained. The heterogeneous sum (19,607) is computed by two methods which provide a check: by summing the five items in the village inventory, and by taking the house total, doubling it twice, and adding these three numbers. The entire procedure was performed using only simple addition, by virtue of the properties of the geometric progression." Several other problem containing sevens has occurred throughout time including in the writings of Fibonacci, and in the well-known children's rhyme of Mother Goose.
The history of exponential functions continues into what we know as compound interest and doubling time. "A Louvre cuneiform tablet from around 2000 B.C. asks the question, "how long does it take an amount invested at 20% annually compounded interest to double itself?" The tablet outlines the entire solution using a tabulation of (6/5)n. From linear extrapolation between n=3 and n=4 the correct answer is 3 years 9 and 4/9 months. This means that compounding interest has been around for a long time! Can you imagine if that investment was still earning interest? Whoever owned that account will have accrued quite the sum of money.
A bit about the number e. As O'Conner states in an article entitled The number e, "The number e first comes into mathematics in a very minor way. This was in 1618 when, in an appendix to Napier's work on logarithms, a table appeared giving the natural logarithms of various numbers. However, that these were logarithms to base e was not recognized since the base to which logarithms are computed did not arise in the way that logarithms were thought about at this time. Although we now think of logarithms as the exponents to which one must raise the base to get the required number, this is a modern way of thinking." "Perhaps surprisingly, since this work on logarithms had come so close to recognizing the number e, when e is first "discovered" it is not through the notion of logarithm at all but rather through a study of compound interest. In 1683 Jacob Bernoulli looked at the problem of compound interest and, in examining continuous compound interest, he tried to find the limit of (1 + 1/n) as n tends to infinity. He used the binomial theorem to show that the limit had to lie between 2 and 3 so we could consider this to be the first approximation found to e. Also if we accept this as a definition of e, it is the first time that a number was defined by a limiting process. He certainly did not recognize any connection between his work and that on logarithms."