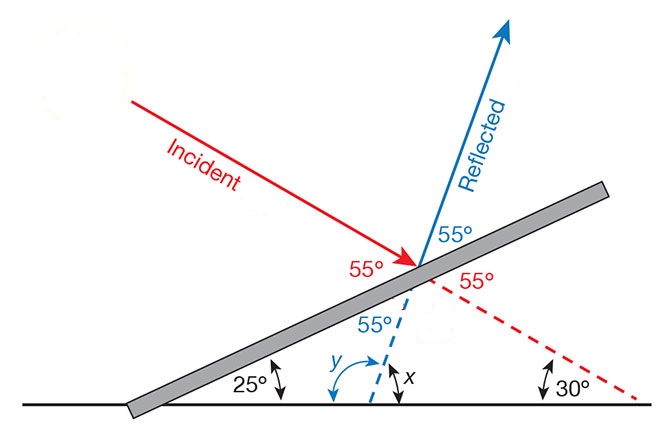
I know that some of you thought of billiards as just a game played on a table with holes and balls. But! now you get to delve into the magic that is mathematics and how it is related to everyday life! First off, mathematicians proved that angle of incidence (the angle in) and the angle of reflection (the angle out) are congruent. This can be proved a couple of ways, but I like using reflections of the table and the corresponding angles to prove this. If you take a table, A, and reflect it across the top wall, forming table B. Also with balls a and b, which will be reflected onto table B, a' and b'. We know the shortest path between any two points is known to be a straight line. So when a line is drawn from a to b' it will give us our angle of incidence. From the point that line intersects with the top wall of A we can draw a reflected angle which will intersect with b, creating our angle of reflection. Now to assign angle measurements to ones we have created. The angle of reflection we will call θ. Now we know from our construction of the reflected table B that our reflection angle, θ, is the same on B. And θ is a vertical angle to our incidence angle. Since we know vertical angles are congruent we conclude that our angle of incidence and reflection are congruent. Fig 1 below shows a similar construction.

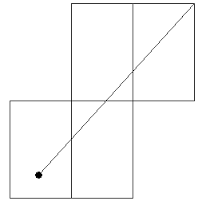
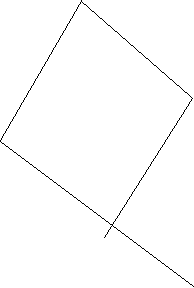
For now we are just going to focus on rectangular billiards. Mathematicians also figured that when the cue ball is shot at a specific angle, in this case 45 degrees, and they followed the path of the ball. But instead of measuring each angle they discovered what they call the “unfolding method”. The method begins by reflecting a rectangle to the right of our original rectangle, then another above the second rectangle and then finally another reflection to the right of the third rectangle. Finally we draw a line from the ball, which is two feet from the base of the original table, to the most top right corner of the fourth reflected rectangle. (Fig 2) Similar to the way we drew our construction for the reflection angle proof the consecutive reflection angles will be constructed the same way. (Fig 3)
Reflections can be expanded upon while still relating to billiards as a whole. Going back to the "unfolding method", when we do that to map a path and "fold" it back up each wall has been duplicated n amount of times. When looked at on just one rectangle if an object could continue through a wall that it hits it would come out the opposite side. (A common video game played called "Snake" is an example of this theory.) So if we take a rectangle with sides Xand Y and we expand our thinking using this theory, essentially the X sides are the same and we could roll this plane into what would become a cylinder. This cylinder is a three-dimensional shape, and now if we do a same process to both top and bottom of the cylinder, Y, we would make a donut shape, or a torus to be more precise. This connects what we have worked with just straight lines and drawing straight lines within a torus. This introduces a periodic orbit idea. In a rectangular billiards table, mathematicians have found that when a ball is hit so that is forms a 60 degree interior angle, the ball will at most hit six different places on the billiards table. That would also mean the incidence angle and reflection angle would measure 60 degrees in order to form a 180 degree angle (i.e. the wall of a billiard table). They prove this by again reflecting and duplicating angles that measure 60 degrees. You can get at total of six 60 degree angles before you start repeating. In other words, 6 X 60 degrees = 360 degrees, which is a complete circle or period, and the ball will begin to retrace its original path. However, this case is generally for a frictionless table and without loss of generality the ball will not lose any momentum from deflecting off the walls of the table. This started getting mathematicians to start thinking about different shapes of billiards tables. Polygonal billiards started mathematicians experimenting more with periodic orbits. A finding that has been agreed upon is that in a triangular billiard table, as long as all the angles each measure to be less than 100 degrees, then there would be at least one periodic orbit, however if that stipulation is not met, there is no agreement as to if there would be a period orbit or not. The way our triangle example had formed a periodic orbit, when the hexagon that all six triangles would form when put together could be deconstructed to form the shape of a rectangle. This deconstruction process is similar to the process used to make the torus in the first place. And we know that once we get a rectangle we can then form a torus from that. Therefore, resulting in a periodic orbit.