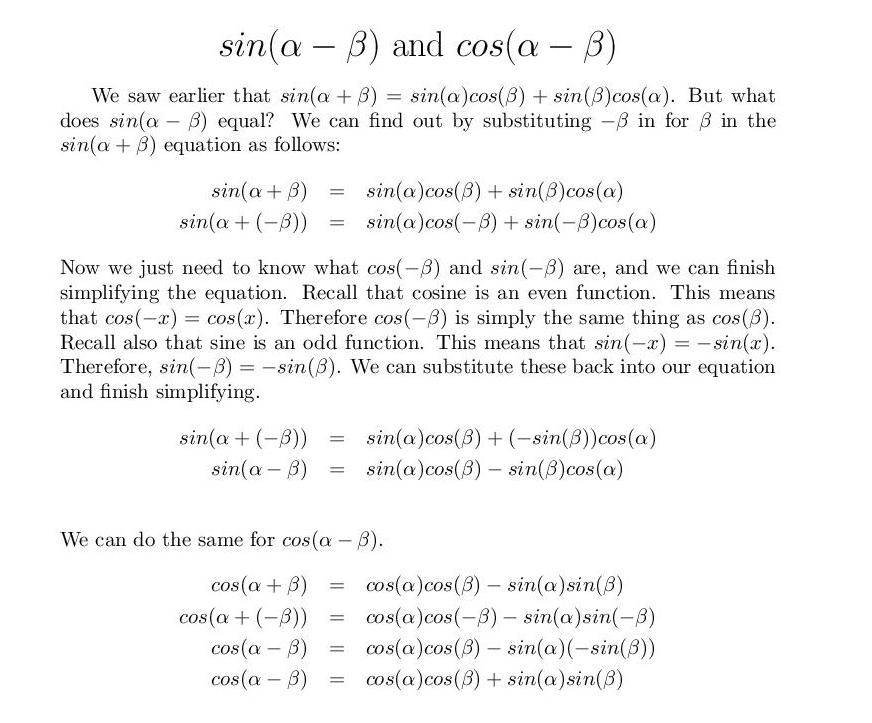Sum and Difference Identities
The sum identities, in my opinion, are the first pillar identities in trigonometry. Most other identities can be derived from these two basic
identities. These identities are also two of the least obvious, at least to me. "That the cosine or sine of a sum or difference is not the sum or difference
of the cosines or sines is easy to establish by counterexample. However, the actual expansions for cos(A+B), cos(A-B), sin(A+B) and sin(A-B) are not
intuitively obvious for most students. Standard textbooks do cover the derivations of these expansions, but the results have a greater impact if
students conjecture them first." (Hurwitz, 2002, p. 510) I couldn't agree more. I think students need to see where these come from, and make their own
conjectures.
While doing this project, I came across a geometric proof of the sum identities for sine and cosine. Below are applets demonstrating these proofs. I think
there is power in seeing things geometrically. Guanshen Ren, a math teacher, said, "Studying trigonometric identities from a geometric perspective helps
students make connections among various branches of mathematics and raise students' interests and appreciations in geometry." (1995, p.24) I have personally
found these proofs very helpful. I think it important for students to understand that these came from somewhere specific, and to be able to use them. I am
not a big fan of memorizing equations, but I do believe that the sum identities are two that would be worth committing to memory.
Geometric Proofs of the Sum Identities:
Deriving the Tangent Sum Identity:
Difference Identities:
References:
-
Hurwitz, M. (October 2002). Cos^2x+sin^2x and the Trigonometric Sum
and Difference Identities. The Mathematics Teacher, 95(7), 510-514.
Retrieved from http://www.jstor.org/stable/20871135.
-
Lei. n.d. An elementary proof of two formulas in trigonometry. math.wisc.edu. Retrieved November 12, 2013. From http://www.math.wisc.edu/~leili/teaching/math222s11/problems/quizzes/trig.pdf.
-
Ren, G. (January 1995). Match Geometric Figures with Trigonometric Identities. The Mathematics Teacher, 88(1), 24-25. Retrieved
from http://www.jstor.org/stable/27969162.