When we think back to our early years of math, how much do we actually remember? It seems that a lot of the content we are taught goes in one ear and out the other, except parabolas. Parabolas tend to be a large part of what we remember from math classes. This can be from how it was taught, when it was taught, or the fact that it is such a large concept that helps us develop understanding of other mathematical concepts in later years.
A parabola can be defined by the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface
(Wikipedia) or a locus of points in a plane which are equidistant from a given point (the focus) and a given line (the directrix)
(Wikipedia). The discovery of parabolas came through the exploration of a cone. Menaechmus was studying a cone sometime in the years of 300 BC. As he studied the cone he discovered different curves existing in conic sections. The cone could be split into sections that either showed parabolas, hyperbolas, ellipses, or circles. Many mathematicians found that parabolas could be used for many different things. Pascal considered it a projection of a circle, Galileo showed that things follow parabolic paths, Menaecchmus attempted to duplicate (double the volume of) a given cube, and much more.
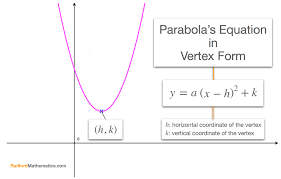
As more scientists continued to develop their understanding of motion and gravity, they were able to form the idea of a parabola and its equation. The equation for parabolas can be written in multiple ways:
\[y=a(x-h)^2+k\]
where (h,k) is the vertex of the parabola, or standard form which is written as
\[y=ax^2+bx+c\]

From the discovery of and creation of parabolic equations, mathematicians were able to create parabolas in a 3D space. These 3D parabolas are known mostly as paraboloids but there are other types in a 3D space such as parabolic cylinders. Parabolic cylinders can be described by The Rejbrand Encyclopædia of Curves and Surfaces as in \[IR^3\] a parabolic cylinder is a set of points (x,y,z) satisfying the equation
\[z=ax^2\] for some \[a ≠ 0\] Each intersection with a plane y=c is a parabola, and all such interactions are identical except for translation in the z direction.
(Andreas Rejbrand, 2022)
This equation can be written 4 different ways because z must be involved in the equation in some way. The possible equations are \[z=y^2\] \[z=x^2\] \[x=z^2\] \[y=z^2\] If the equation does not involve z, then it is making a simple parabola, meaning that it can be graphed on a 2D rather than a 3D graph. This is why the shape is still technically 2D.
An easy explanation of this is imagining it as a surface or a net of a 3D shape. Just looking at it, one should be able to calculate the area if they were able to take it from the graph and lay it on a piece of paper. For example: if we take a piece of paper and slightly wrap it, so that it is making a curved shape, then we can consider this a parabolic cylinder because it is 2D in a 3D space. We can see the similarities between the 2D parabola and 3D parabolic cylinder. The equations both need to contain only two variables. When looking at the 3D shape, if we cut the cylinder multiple times, we are creating a bunch of the same parabola which is why the equations are so closely related.
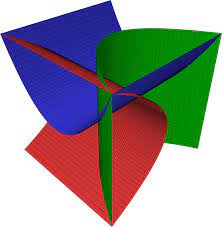
Parabolic cylinders also do not need to be perfect parabolas, they can be what is called distorted parabolic cylinders
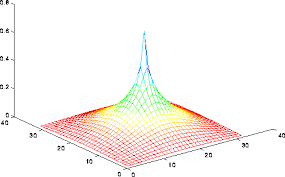
. That just means that they have a minimum ridge in the domain, there is only one ridge or curve on the surface. This keeps the parabolic shape without becoming an equation that involves more variables/terms. In an experiment, scientists use 3D graphs to show data and said that parabolic cylinders can be beneficial to check the data.
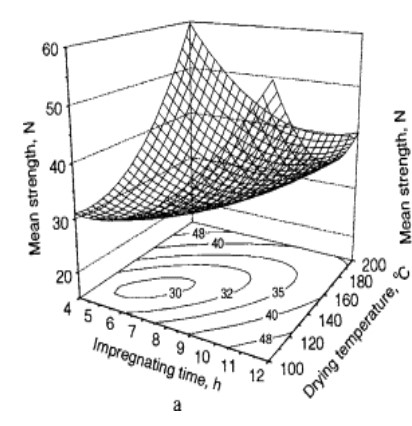
To facilitate a straightforward examination of the effects of the factors, three-dimensional response surfaces and their corresponding contour pilots were constructed using the models developed, with two factors kept at zero level and changing the other two in the design domain. These figures can be used to predict the responses for different values of the factors and to identify the interactions between the factors.
(D. Wu, Y. Li, 2000)
Through parabolic cylinders, scientists are able to analyze two of the three variables of data and see how each one corresponds with another.
Although we see parabolic cylinders in a coordinate system most often, there is also a significant amount of studies for parabolic cylinder functions in math, science, physics, etc. The parabolic cylinder functions are special functions. They are solutions to a specific differential equation. This equation comes from when the separation of variables is used in Laplace's equation. If we were to express this on a coordinate system, it would result in a parabolic cylinder. The standard form of differential equation is:
Similar to both parabolic equations that we have looked at so far, there are only two variables (x and y) in the equation. There are multiple forms for this equation which are made by completing the square including:
\[\frac{d^2y}{dz^2}-(\frac{1}{4z}^2+a)y=0\] \[\frac{d^2y}{dz^2}+(\frac{1}{4}z^2-a)y=0\] \[\frac{d^2y}{dz^2}+(v+\frac{1}{2}-\frac{1}{4z^2})y=0\]
All of these equations can be used the same way and each equation is a function of z and a or v.
The simpler explanation can be described as the parabolic cylinder coordinates are solving partial differential equations. When Laplace's equation is shown through parabolic cylinder coordinates. This leads to the separation of variables through the equation. We are able to get the parabolic cylinder function from this process happening.