The significance and applications of Pascal's Triangle are found within the construction of it and in some really interesting patterns. To start, we are able to solve both combinations and binomials using solely the outputs in Pascal's Triangle. This avoids the lengthy algebra I discussed earlier. (below are some examples)

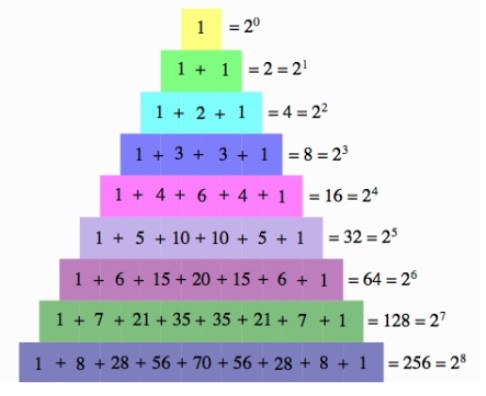
We are also able to find some really interesting patterns. The first of which is that all of the rows add up to successive powers of two. (image shown below)
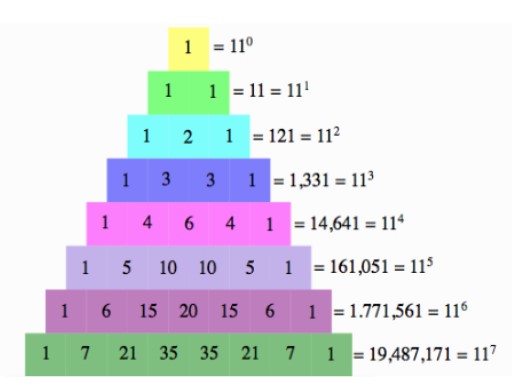
The second of which is a similar idea, however, this time using the idea of decimal expansion. In row two we have 1, 2, and 1. To find this unique pattern multiply the first one by 1, the second by 10, and the third by 100. (1 x 1)+(2 x 10)+(1 x 100) = 121 = 112. In row five this would look like (1 x 1)+(5 x 10)+(10 x 100)+(10 x 1000)+(5 x 10000) +(1 x 100000) = 161,051 = 115. Using the idea of decimal expansion with addition we are able to see how each row is 11n where n is the row number. (image shown below)
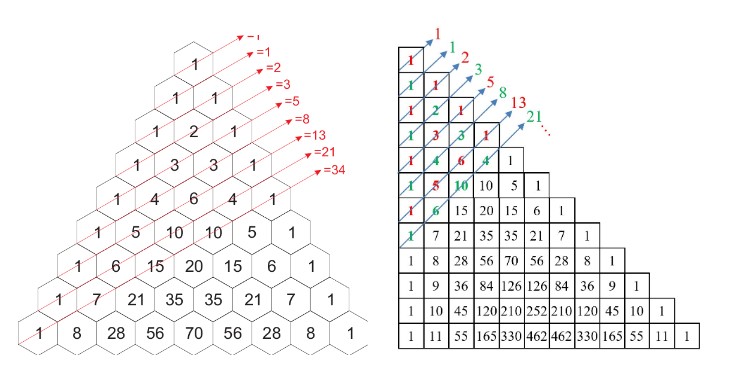
Another pattern of Pascal's Triangle is found within Fibonacci Numbers. "The Fibonacci sequence [is] the sequence of numbers 1, 1, 2, 3, 5, 8, 13, 21,..., each of which, after the second, is the sum of the two previous numbers; that is, the nth Fibonacci number \(F_n\)= \(F_{n-1}\)+\(F_{n-2}\)," (Hosch, 2023). The easiest way to find the Fibonacci sequence in Pascal's Triangle is by tilting the triangle. However, as shown in both the images below you can do it with tilting and without. Drawing lines diagonally, the numbers add to the sequence of Fibonacci numbers.
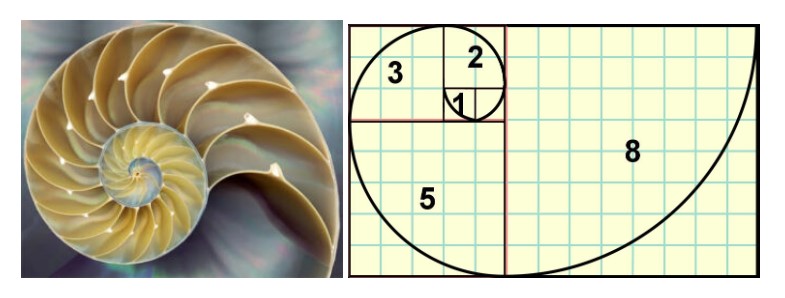
These unique numbers play a large role in even nature and are common in the spiral formation as demonstrated below.
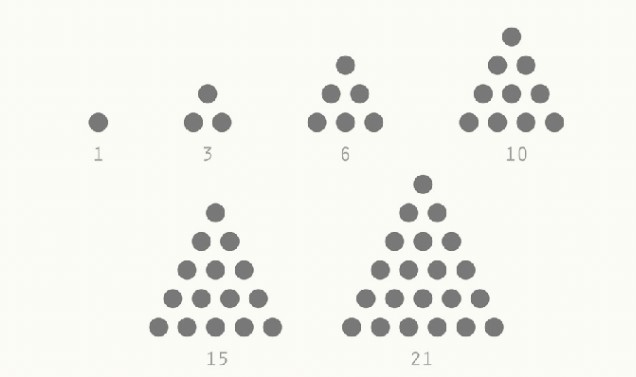
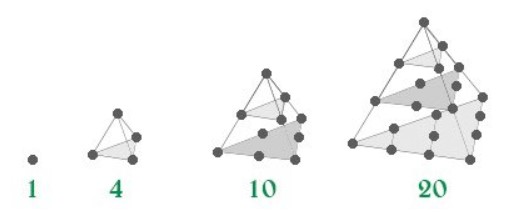
Next, look at the diagonals in Pascal's Triangle. The first two diagonals aren't very interesting. The first is all ones and the second contains the natural numbers. However, the third diagonal contains the triangular numbers. If you take one of those numbers and have that many dots, you will be able to stack them into equilateral triangles. The next diagonal has tetrahedral numbers. Similar to the previous, you can stack that many dots into a tetrahedron. (both equilateral triangles and tetrahedra examples below)
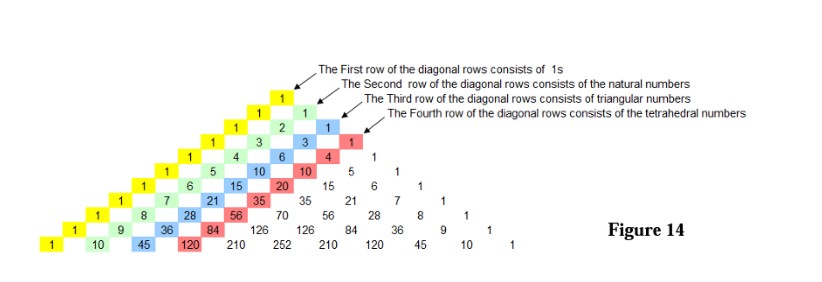
equilateral triangles
tetrahedra
If you want to play with triangular numbers you can use this applet below. (n represents the input into the following equation, \(\frac{n(n+1)}{2}\))
Lastly, shade in all the odd numbers. It doesn't look like a lot when the triangle is small, but when you add more and more rows you get a fractal known as Sierpinski's Triangle. "If you shade all the even numbers, you will [also] get a fractal. This is...the recursive of Sierpinski's Triangle," (Berryman, n.d.).

There are numerous significances and applications within Pascal's Triangle, which was constructed by simple addition. These significances and applications are only just the surface.