There isn't just one way in which to construct Pascal's Triangle. Due to the numerous patterns involved in this triangle, there are numerous ways to construct the triangle. The first way is by far the easiest. "Start with one and imagine invisible zeros on either side of it. Add them together in pairs, and you'll generate the next row," (Ratemi, n.d.). Do that again and again until you are satisfied. You will get a start to Pascal's Triangle, but will never finish due to the fact that the triangle goes on to infinitely. "Pascal's formula shows that each subsequent row is obtained by adding the two entries diagonally above," (Pascal's Triangle -- From Wolfram MathWorld, n.d.). (process shown below)
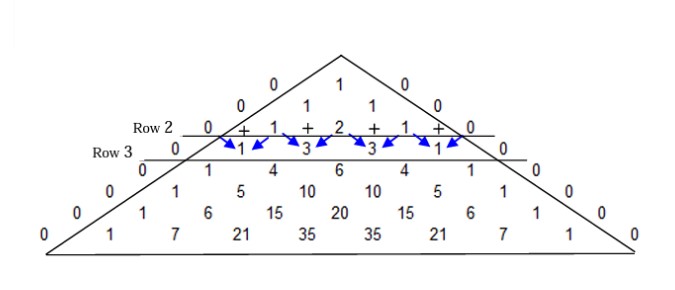
The zeros are not officially a part of Pascal's Triangle and are omitted from the official triangle. They are solely used for the purpose of constructing the triangle. (Pascal's Triangle is shown below)

If you are struggling to understand this type of construction, use this applet.
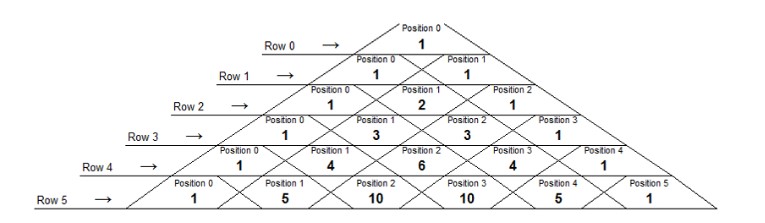
The second way to build this triangle is in terms of combinations. It is important to note that when numbering the rows, the top row is counted as row zero and the next is row one, and so on. When counting the position of the numbers within each row, start from the left, and the first number is in position zero, then position one, and so on. (the counting of rows and position within the row is shown below)
An entry, or position, in Pascal's triangle can use the format C(n,r) or \(\binom{n}{r}\) for combinations. This is read n choose r, where n is the row number and r is the position within the row. For example: C(3,0) refers to row 3 and position 0 within that row. (Pascal's triangle in the \(\binom{n}{r}\) format is shown below)

Use this original applet to investigate the patterns discussed.
"The study of combinatorics is a branch of mathematics that studies finite or discrete structures and includes...combinations," (Leavitt, 2011, 8). If we start with a set of n objects and ask how many ways we can select a subset of r objects, we are asking how many combinations are possible. Note that the order in which the objects are selected does not matter.
An example of this is as follows: "A class of twenty students decides to have a President, Vice President, and Secretary. How many ways can the positions be filled? One way to solve this is to think of three positions. The first has twenty possibilities, then the second would only have nineteen possibilities, and the third position has eighteen possibilities.
20 x 19 x 18 = 6,840 ways to fill the roles of President, Vice President, and Secretary
Another way to solve the problem is to find the number of ways to arrange all twenty students and the number of ways to arrange the seventeen students who will not be filling the position. Then divide the number of ways to arrange all twenty students by the number of ways the seventeen students are not filling positions. The number of ways to fill just the three positions will be what remains.
\(\genfrac{}{}{1pt}{3}{\Large\text{ways to arrange 20 students}}{\Large\text{ways to arrange 17 students}}\) = \(\genfrac{}{}{1pt}{3}{\Large\text{20!}}{\Large\text{17!}}\) = \(\genfrac{}{}{1pt}{3}{\Large\text{20 x 19 x 18 x 17!}}{\Large\text{17!}}\)
= 20 x 19 x 18 ways", (Chenoweth, 2022, 7).
Listing all the possible combinations is tedious and it becomes very easy to make a mistake and miss options. This is where the formula becomes very useful. C(n,r) = \(\binom{n}{r}\), where \(\binom{n}{r}\) is defined as \(\frac{n!}{r!(n-1)!}\). If we solved every single combination as shown in the \(\binom{n}{r}\) formatted Pascal Triangle, we would be able to find Pascal's Triangle as we discovered at the beginning. Blaise Pascal worked closely with Pierre de Fermat within combinations which was the start of creating the branch of mathematics we have today: probability theory. Probability theory is the branch of mathematics concerned with probability and it uses this idea of combinations which are used in scenarios like the one listed above.
The third way we could construct this triangle is by using binomial coefficients by solving the equation (a+b)n for any n≥0. n represents the row and the order in which the coefficients appear are the positions of the row. "The entries in Pascal's Triangle are called binomial coefficients since they are the coefficients upon expansion of (a+b)n," (Austin, n.d., 1). (a few examples are calculated below with all coefficients explicitly written)
(a+b)0=1
(a+b)1=1a+1b
(a+b)2=1a2+2ab+1b2
(a+b)3=1a3+3a2b+3ab2+1b3
(a+b)4=1a4+4a3b+6a2b2+4ab3+1b4
In row 0 there is just 1. In row 1 there is 1 and 1. In row 2 there is 1, 2, then 1. In row 3 there is 1, 3, 3, then 1. In row 4 there is 1, 4, 6, 4, then 1. This continues on and on to fill Pascal's Triangle rows. It is also important to recognize the pattern within the variables themselves. Reading left to right, a starts with an exponent of m, where n=m, and works its way down one by one until it gets to zero. Reading left to right, b starts with an exponent of 0 working its way up one by one until it reaches m. Recognizing this pattern will allow me to find these binomials without any ridiculous algebra.
Most likely you wouldn't necessarily use combinations and binomial coefficients to build the triangle, but it is useful to recognize this path to ease the solution process. Binomial coefficients are used in the Math 3 Core Standards. Pascal's Triangle is taught in order to help students find the solutions without lengthy algebra.