Topology is a field of mathematics that uses definitions of equivalency in reference to objects that can be called "the same" if they can be continuously deformed into one another. This is done through methods of stretching, bending, twisting, and shrinking with a special emphasis being placed on the fact that nothing is added or torn away. This is further subdivided into different topologies, some of which include algebraic topology, general topology, discrete topology, and differential topology, all of which explore different aspects of the world in relation to mathematical abstraction. Furthermore, "Applications of topology are different from applications of other areas of mathematics. The utility of topology comes from its ability to categorize and count objects using qualitative "approximate" information as opposed to exact values. Our primary criteria in choosing applications is to look for questions from outside topology whose solution involved topology and would have been either significantly more difficult or impossible without topology" (Basener, 2006). This means that topology is a branch of mathematics that seeks to categorize objects in ways that allow for methods of problem-solving that would otherwise not be possible. Additionally, topology is a field of mathematics that is still being explored with many of the concepts explored and explained not having real-world applications due to the lagging of either technology or people not knowing how to apply the math yet.
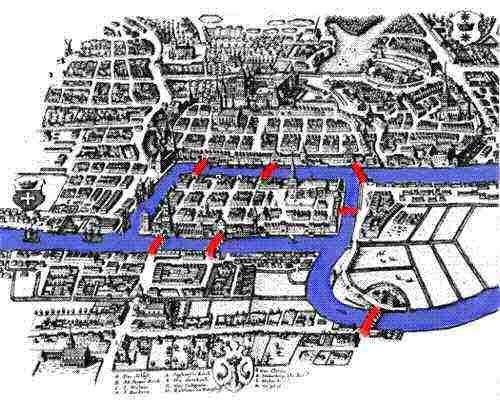
Historically one of the first cases of topology was with Leonard Euler with a problem called the "Konigsberg Bridge Problem". In the 18th century, the city of Konigsberg was a center of trade located along a river. In this city, there were seven bridges connecting an island to 3 different banks, as pictured below.

People wanted to know if you could cross each bridge only once in a trip across the city and arrive at your starting point. The city asked Euler and, intrigued, he came up with a proof for its impossibility (Paoletti, n.d). This is considered the informal beginnings of topology, where we are working with a shape and the categorization of paths that can or can't be walked.
The field of topology is a relatively new emergence, it was the 1895 publication of Analysis Situ by Henri Poincare that finally helped canonize topology into its distinct field of study, though many ideas concerning topology had been a part of mathematics in the previous century and a half (Carlson, 2023). The main fields at the time were algebraic and general topology (also known as point-set topology), with algebraic topology being the focus. This started with "The most basic classes of objects whose properties are studied in A.T. are complexes (or polyhedra): simplicial complexes, cell complexes or other complexes; manifolds: closed or open manifolds, manifolds with boundary" (Novikov, 2004). As these topics were explored, the field of topology flourished in the mathematical community and became a method in which we can categorize and count objects for analysis and computation.
In topology, there are many fields of study, all of which are full and rich topics. It is important to note that many topics can be represented geometrically and whilst geometric topology isn't a distinct field it does intermingle with almost all aspects of topology due to the ability it has to give intuitive understanding.
Algebraic Topology uses the algebraic categorization of topological spaces into different groups, which then leads to the ideas of homology and homotopy. "The basic idea of homology is that we start with a geometric object (a space) which is given by combinatorial data (a simplicial complex)" and "A homotopy is a continuous family h_t:X → Y of continuous maps which depends on a real parameter t ∈[0,1]" (Dieck, 2004). Focusing on homotopy, we can model such changes algebraically, which one of the foundations of algebraic topology, as shown in the applet below.
These ideas drive the theory behind algebraic topology just as homeomorphisms and isomorphisms are foundational in abstract algebra. We can also see this in the example of the torus-to-mug transformation.

This models the continuous change that takes place in a geometric sense and illustrates that things can be homotopic, even if it seems counterintuitive.
Another issue in the realm of topology concerns the idea of manifolds both in lower dimensions and in dimensions higher than the 4th. This starts with low dimensional topology, or manifolds, which are spaces that are recreated in a Euclidean space, for example, latitude and longitude are markers of a curved space and are used to represent a set of coordinates on a 2-dimensional surface. Simply put, "the core of low-dimensional topology has been the classification of knots and links in the 3-sphere and the classification of 3- and 4-dimensional manifolds" (Kirby, 2011). Differential topology is then focused on manifolds of higher dimensions, particularly 5 and above. The goal of differential topology is to answer global questions (Hirsch, 1976). This means that differential topology asks questions about the entirety of the space whereas something like differential geometry asks about local areas. To put a frame of reference we would consider the torus and mug to be the same in differential topology but they would be different objects in differential geometry due to the points having reference to the local space.
With the varied, encompassing nature of topology, there are a variety of applications. Topology has direct applications to both cartography and astronomy, where we can better quantify our existence in different spaces. In addition to this, there are also strong applications in Biology, with topology being particularly useful in the sequencing of DNA. "In topology, we define something called a metric, which is basically a distance function used to measure the distance between the elements of a set. This was the importance of metric spaces in DNA modeling." (Saini, 2022).
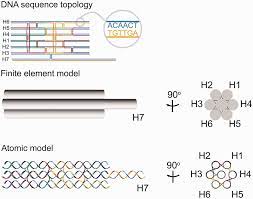
This modeling is what allows us to better understand the genetic makeup of life and can be seen in "As long as the ends of DNA are fixed in space, topological relationships are defined as those that can be altered only by breaking one or both strands of the double helix…..Topological relationships in DNA include underwinding and overwinding, knotting, and tangling." (Joseph E. Deweese, 2008). Through the usage of topology, the structure and subsequently the impact of different phenotypes on an organism can be understood. This could then further be used to help identify genetic defects in individuals for treatment or preventative care.