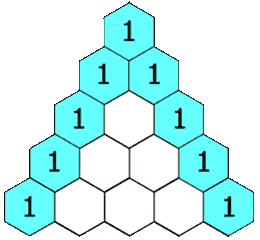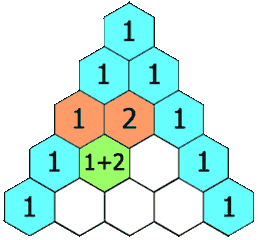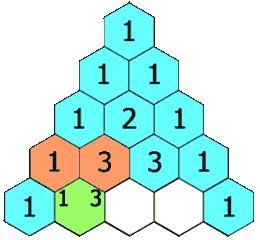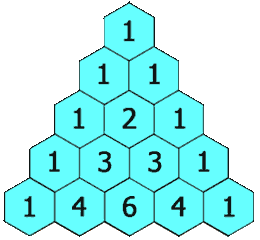
Pascal's Triangle is relatively easy to construct. The top row, called Row 0, starts with a 1. The next row down has two ones. For the next row, add the two 1s above, to get the middle number, 2. The numbers to the side of the 2 are 1's to complete Row 2. The construction of Pascal's Triangle is easier to understand if seen visually, so check out the graphic below for a visual representation.

By Hersfold on the English Wikipedia - Own work, Public Domain, https://commons.wikimedia.org/w/index.php?curid=3902538
There are multiple patterns to be found in the construction of Pascal's Triangle. These patterns produce interesting shapes and concepts that are unique to the triangle. Some are fairly obvious and some are more complex.
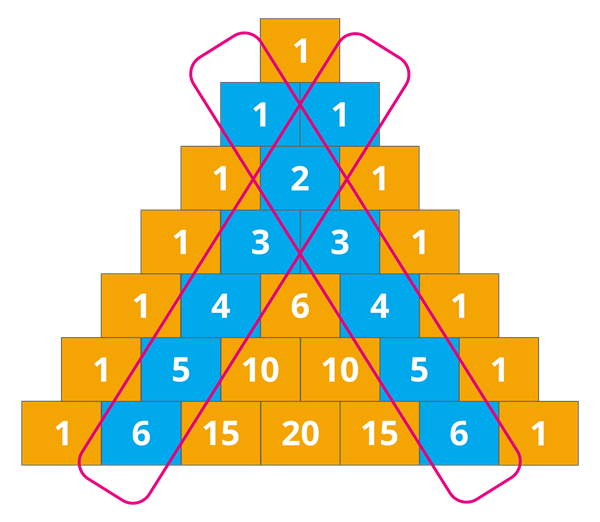
One of the most obvious patterns is the symmetry of the triangle. Splitting the triangle down the middle shows that both sides are equal, and interestingly, this symmetry is caused by how the triangle is constructed. Another simple observation involves the second diagonal on the left and right-hand sides. These diagonals are the counting numbers or the whole numbers, as shown below. (IBDP Student Blogs)
https://www.yaclass.in/p/mathematics-state-board/class-7/information-processing-4019/tables-patterns-and-pascal-triangle-leads-to-linear-function-5428/re-90083971-8468-46a7-b45f-d0ba01e83d6a
The triangle numbers also appear as a pattern in the third diagonal of the triangle. Triangle numbers are numbers that, if the number is represented as elements, the elements form an equilateral triangle which is made by creating rows with one more element than the row before it. These numbers are {1,3,6,10,... }. A pictorial representation of what triangle numbers are is shown below. Refer back to Pascal's Triangle and the third diagonal. Notice how these numbers and the numbers in the traingle match up. (Byju's)
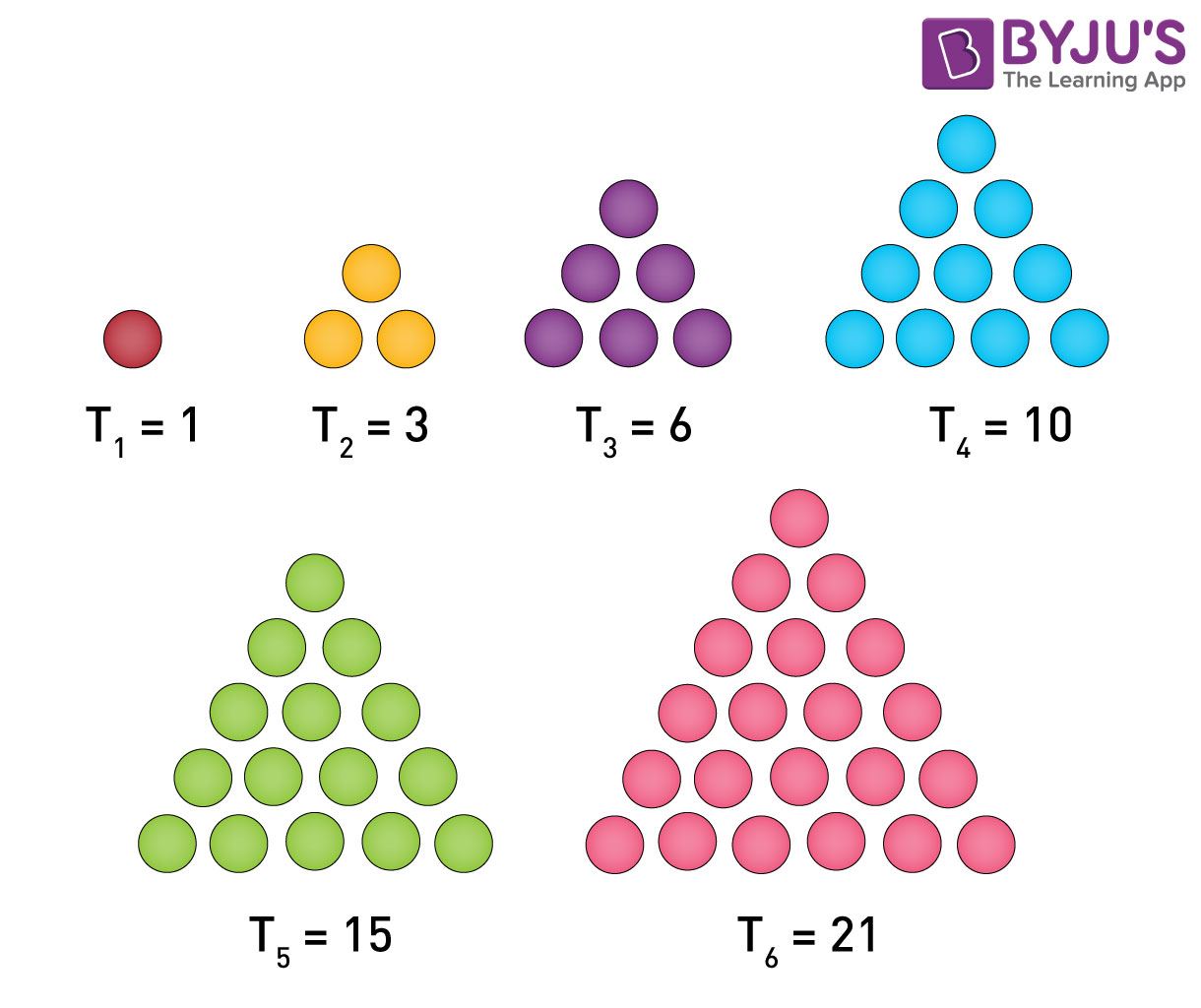
https://byjus.com/maths/triangular-numbers/
Now, find the sum of each row of Pascal's Triangle, with the top row as Row 0. The Row 0 sum is 1, and the first-row sum is 2. The sum of the second row is 4, and the sum of the third is 8. Let the row name be Row n. The formula for finding the sum of the elements in the n-th row of Pascal's Triangle is \(2^n\) (IBDP Student Blogs) . The video below walks through two different proofs of this formula if you are interested in learning more.
Consider that each digit in a row forms a number. For example, row 0 is 1, row 1 is 11, and row 2 is 121. If there is a number with double digits, like 10 in row 5, add the left-hand digit to the previous number for your digit in the final number. So, row 5 becomes 1, 5 + 1, 0 + 1, 0, 5, 1, or 161051. The interesting thing about these numbers is that they are the powers of 11. The number created by the digits in a row n is \(11^n\) (Shute). Engage in the applet below to build see how this pattern appears in the first few rows of the triangle.
Questions for dicovery:
1. Continue the pattern on your own, does this work for all rows?
2. How do you think this pattern is helpful for mathematicians to know?
3. What do you find interesting about the pattern and how it is found?
An explanation and informal proof of why this pattern exists is also given at the link here.
Many visual patterns emerge when multiples of a number are highlighted in the triangle. Consider filling in every multiple of 2 on the triangle. The design created by the shaded numbers is known as a Sierpinski Triangle. This triangle is known as a fractal or a self-similar repeating object. There are three rules of addition to consider: \[even+even=even\] \[odd+odd=even\] \[even+odd=odd.\] When the triangle is being constructed, even numbers are created in the form of triangles because of these addition rules.
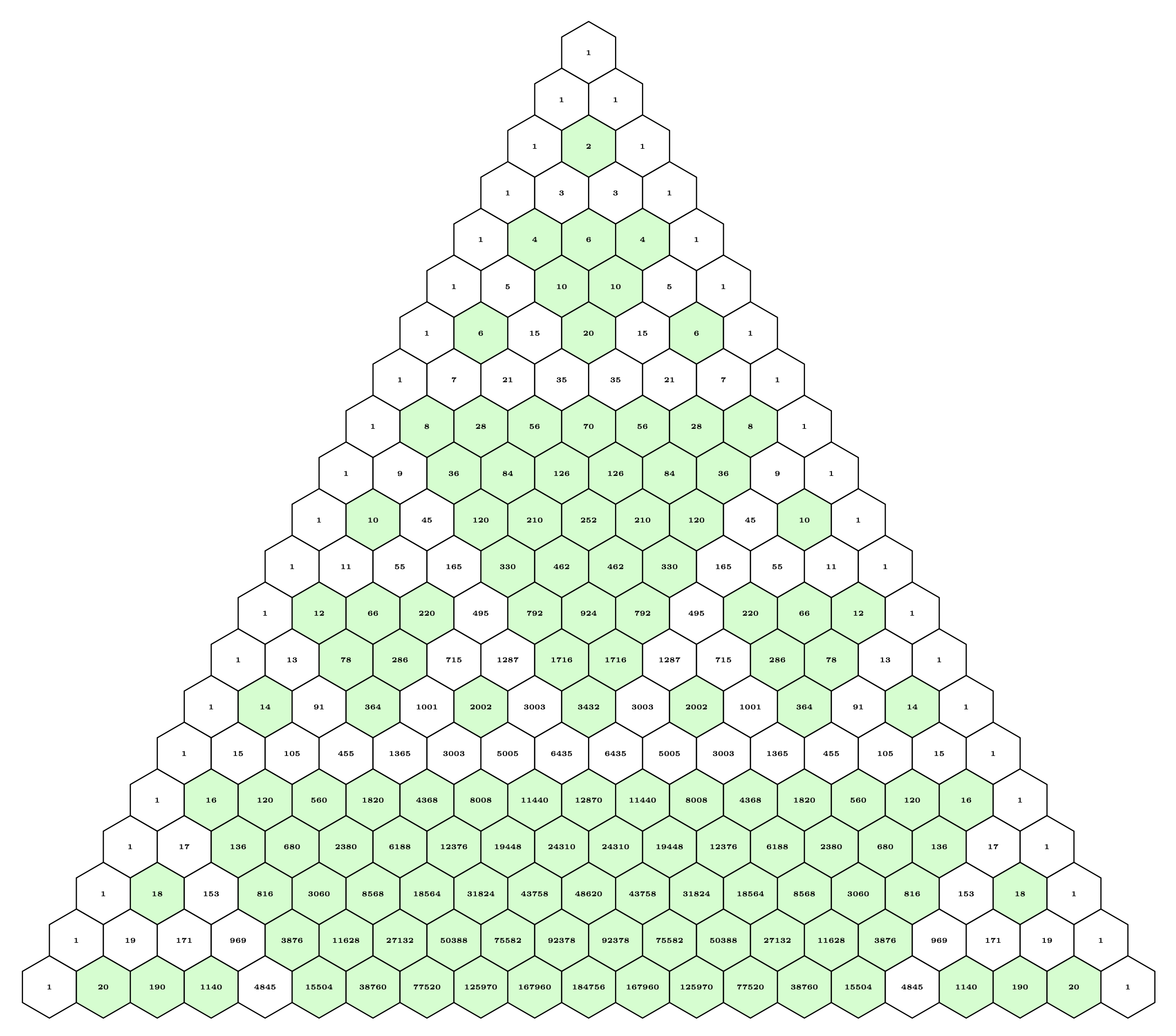
https://tex.stackexchange.com/questions/575092/draw-sierpinskis-triangle-in-pascals-triangle-in-tikz-30-row-or-more
The following applet walks through more patterns that can be found within the triangle. Explore the patterns on your own and make note of any you find interesting or unique.
The patterns may seem like fun but unnecessary discoveries, but they allow mathematicians to make new connections. Each design has multiple proofs and connections that follow. New discoveries lead to new connections.