Trigonometry is a branch of mathematics that studies the side lengths and angles of triangles. The unit circle was created to express these relationships for specific triangles. The term "trigonometry" was derived from the Greek "trigonometria", meaning "triangle measuring." A Greek mathematician named Hipparchus is considered to be the founder of trigonometry. He was given this title because he was the first person to develop a table of trigonometric chords. A chord is a line segment connecting two points on a curve. Chords are important for trigonometry because they are used as another way to figure out side-lengths of triangles. This was an important feat because "the problem was to find the length of the chord subtended by a given angle." (O'Conner). (In geometry, an angle is subtended by an arc, line segment or any other section of a curve when its two rays pass through the endpoints of that arc.) Hipparchus was able to discover a formula that calculates this length. The modern version of this formula is: chord(x) = r(2 sin(\(\frac{x}{2}\))). He then used this knowledge to generate a table with the values for the chords. Advancements like this allowed precise measurements and calculations on a level unknown beforehand.
Trigonometry was historically developed for astronomers and geographers. The stars were thought to be fixed points on a very large sphere, with only the planets moving. Spherical trigonometry was used to understand the positions on a sphere. Menelaus' work on spherics is the earliest known work on spherical trigonometry. Spherical trigonometry is rarely taught in schools because it has been replaced with linear algebra.
Navigators used something called an astrolabe (that looked like a compass) to measure the angle between a star and the horizon. They would consider the time of year (because stars change depending on the time of year) and use a couple of reference points and a star chart to determine where they were located on the earth. The astrolabe was used for measuring the position of the sun and other starts to help aid in navigation.

A coordinate is specified by a combination of two angles, one north or south from the equator (0 degrees), and one east or west from the prime meridian (crossing through Greenwich England). This constitutes latitude and longitude. Using two perpendicular lines like latitude and longitude to describe a certain point in space sounds very similar to an x, y coordinate plane used by the unit circle. Each point on the unit circle is described by its x and y direction, or rather, its latitude and longitude. The modern compass, which was designed to help navigate these latitudinal and longitudinal lines, looks like a unit circle if positioned sideways.
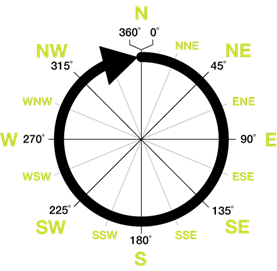
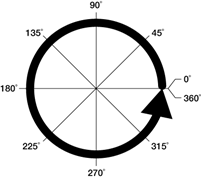
When the unit circle was being created, there were many factors to consider. For example, what are the most important angles to show? Where should the unit circle start, and should it go clockwise or counterclockwise? For navigation, they place 0 at the top of the circle because that is straight ahead for them. However, for the unit circle, the starting place may have been determined based on how the x,y coordinate plane system was set up (causing (1,0) to be the starting coordinate). Regardless of how it was decided, it is convention for counterclockwise to be positive in the unit circle.
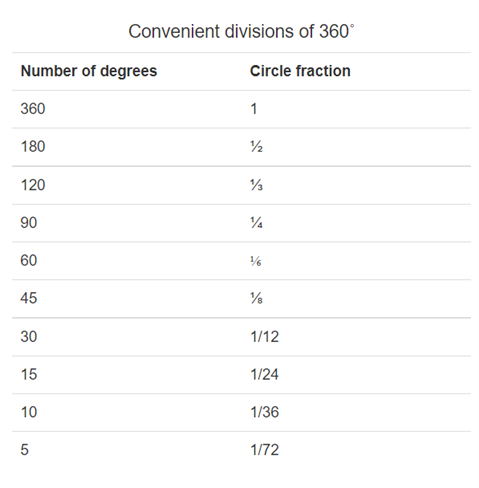
There were many other questions, such as how many sections should a circle be divided into? We all know that it was divided into 360 sections, but why couldn't it have been divided into an easier number like 100? While there are many things about the creation of the unit circle that we don't know, there is a definitive answer for this question. Jeff Cruzan explains, "it turns out that numbers like 360° and the 60-minute hour likely arose because of the convenience of using fractions of those numbers. While 100 can be divided into 50ths, 10ths, and so on, 60 can be divided sections of \(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\), \(\frac{1}{6}\), \(\frac{1}{10}\), \(\frac{1}{12}\), and a few more convenient fractions. It made a lot of sense before the digital age" (Cruzan).
Top of page