Koch's Snowflake

Fractal Geometry can be represented through mathematical functions and equations. However, it can be used conceptually and through different figures to then represent other mathematical anomalies and problems.

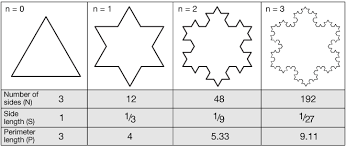
One of the more famous snowflake fractals in Mathematics is known as the Koch Snowflake or the Koch Curve. This fractal holds very special properties that hold to the characteristics and thought process of Mandelbrot's ideals when he derived the idea of fractals with his problem of the Coast of Brittany. Koch's Snowflake is constructed with equilateral triangles of varying size. To begin the construction process, one will start with a single equilateral triangle, this is the zeroth iteration. An iteration is essentially the next step or next set of added on triangles, as shown in picture below you can see the first three iterations. The next iteration begins when three smaller and congruent equilateral triangles are added (see when n=1). Each of these triangles' side lengths are one-third that of the side that it was added to. For example, if the equalateral triable for iteration zero has a side length of 6, the itteration one triangle would have side lengths of 2.

With every iteration, more and more congruent equilateral triangles are added and will go on forever. It is interesting to observe what properties the area and perimeter show. Let's first take a look at the area as each equilateral triangle is added. With every iteration, the area does continue to increase, however this increase converges meaning it can only grow to be 1.6 times bigger than the original area. Thus, as the number of iterations increases, the total area that is being added is practically zero. On the other hand, the perimeter has another story. Watch the video below to see how.

Below is an applet so you can go through the first 4 iterations at your own pace and observe the properties shown. Use the slider to increase the iteration number to add more triangles. Then observe the area and perimeter calculation on the side. After reaching the 4th iteration, check the boxes under the calculations.

Use the following links to explore more of the mathematics of Snowflakes and Fractals!