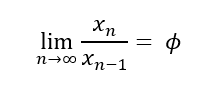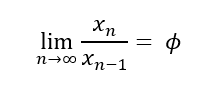Fibonacci and Phi
Introduction
Geometry
Fractals
Beyond Nature
“The Fibonacci Sequence turns out to be the key to understanding how nature designs... and is... a part of the same ubiquitous music of the spheres that builds harmony into atoms, molecules, crystals, shells, suns and galaxies and makes the Universe sing.”
–Guy Murchie
History
Fibonacci

Leonardo of Pisa—known by many other names, famously Fibonacci—was born in 1175 and is considered one of the most important mathematicians of all time. He had many great accomplishments in the field of mathematics, but one that is of note is his Fibonacci sequence and how that sequence can give us the golden ratio, phi (ɸ). The Fibonacci sequence is likely his most well-known contribution and can be shown as the sequence 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, … where you get the next number in the sequence by adding the two preceding it. This could also be written by a recursive equation:
\[x_n=x_{n-1}+x_{n-2}\]
This sequence shows up in different ways throughout nature, especially in the form of the golden ratio. The golden ratio was known by the Greeks and Egyptians thousands of years before Fibonacci even lived (Debnath, 2011). Then and now, it is a useful tool to study the math involved in nature. The golden ratio is explained more thoroughly on the math page.
Explanation/Application of Mathematics
Golden Ratio/Fibonacci Sequence

Debnath explains that “the golden ratio (or the golden number or the golden section) is defined by dividing a line segment AB=a by the point C… into two unequal parts x and y(less than x) in such a way that the ratio of the larger part x to the smaller part y is equal to that of the total length x+y(=a) to the larger segment x” (Debnath, 2011). In simpler terms, the golden number is the ratio of the smaller side of the segment, x, to the larger side, y, such that x/y=1.61833988...=ɸ (phi). This can then give golden sections, golden spirals, golden rectangles, etc. all of which can be found in nature. The way that Fibonacci connects to this is because the golden ratio can also be found using Fibonacci numbers (Debnath, 2011). By dividing each term in the Fibonacci sequence by the one preceding it, these ratios begin to converge closer and closer to phi. In other words when we take 1/1, 2/1, 3/2, 5/3, 8/5, 13/8,..., we see that the numbers become closer to 1.618… Using the notation that we did previously to represent the Fibonacci sequence, this could be represented as:
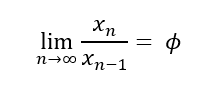
Dürer Pentagon
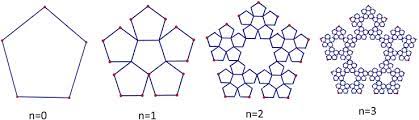
The Dürer Pentagon combines the ideas of the golden ratio with fractals. Albrecht Dürer created this shape based on a regular pentagon where then “in each iteration each pentagon is divided into six smaller pentagons and five isosceles triangles, and the triangles are removed” (Bunde & Havlin, 2013). Each of these inner triangles exhibits the golden ratio between its shorter and longer sides. Multiple iterations of these pentagons will begin to resemble snowflakes, which follow both fractal and golden ratio patterns.
Spirals


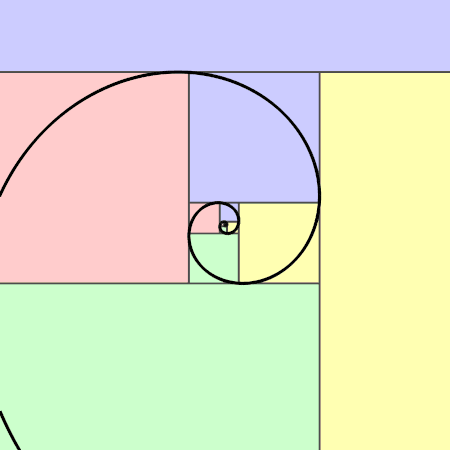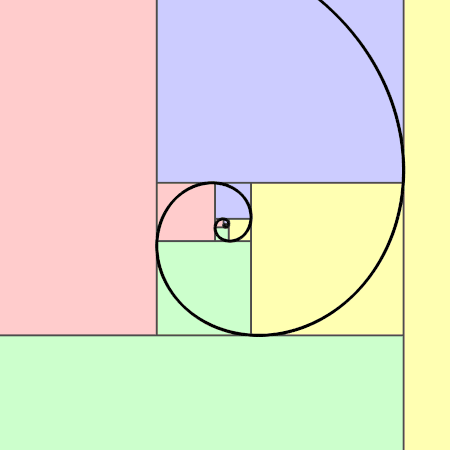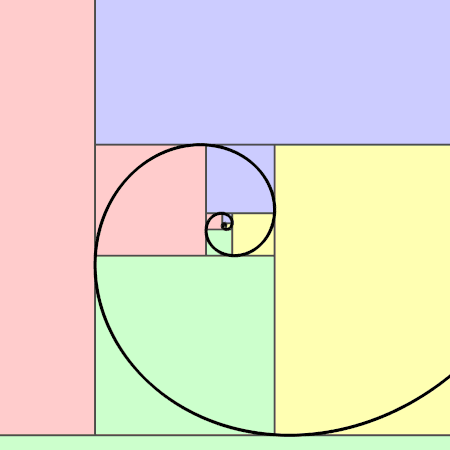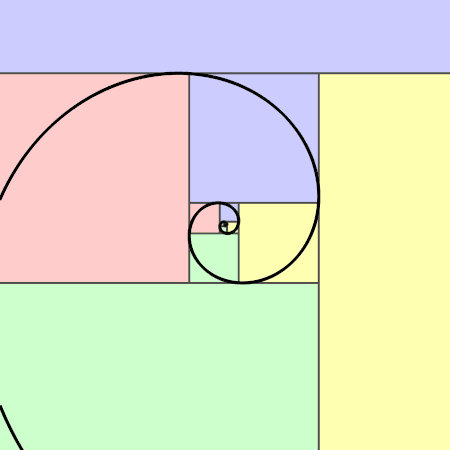
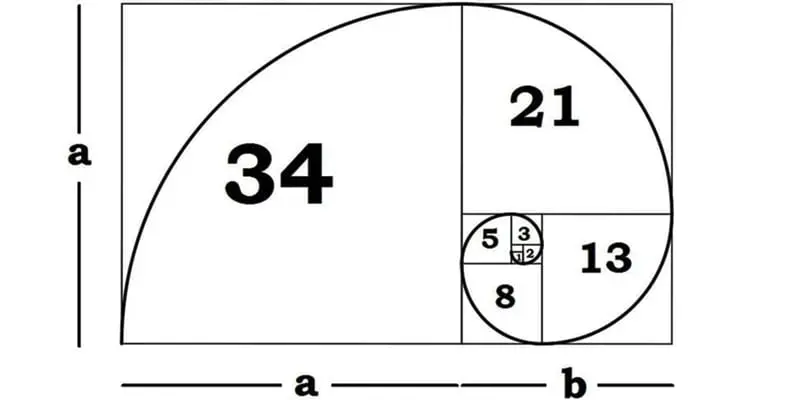
Spirals also combine these two concepts. A golden spiral can be drawn using a golden rectangle. To first construct the golden rectangle, several methods can be used. One option is to draw a square with side length of 1. The next square would also have side length of 1 and would join the last square. The next square would have a side length of 2, the next a side length of 3, then of 5, of 8, of 13, and so on with side lengths following Fibonacci numbers. These squares all together would form a golden rectangle. Drawing quarter arcs to connect the corners of each of these squares would produce a golden spiral that kept the proportions of the golden ratio (Akhtaruzzaman & Shafie, 2011). These spirals appear throughout nature, for example in pinecones. Akhtaruzzaman and Shafie explain that “the spiral happens naturally because each new cell is formed after a turn. Plants grow new cells in spirals format and this pattern is seen on the seeds arrangement of the beautiful sunflower, orange petals, seed florets, pinecones, broccoli and even in the petals of rose”.
References