Moving forward to the actual mathematics involved in infinity, Cantor’s hypothesis leads perfectly into the topic of elements in an infinite set. The two different infinite sets are countably infinite sets and uncountably infinite sets. A countably infinite set can be described as, “Any set which can be put in a one-to one correspondence with the natural numbers (or integers) so that a prescription can be given for identifying its members one at a time… Once one countable set S is given, any other set which can be put into a one-to-one correspondence, or in other words a bijection, with S is also countable. Countably infinite sets have cardinal number aleph-0” (Weisstein). A cardinality of a set refers to the number of elements in a given set. If we look at a set of natural numbers, we know this is an example of a countably infinite set. In a set of natural numbers, we could have (1,2, 3,…). In this set, we are able to never stop counting numbers. Relating back to Cantor, he used ℵ0 which means ‘aleph null’ as the symbol which represents the cardinality of the set of natural numbers. When discussing further on the topic of cardinality, in set theory two sets have the same cardinality when we are able to create a one-to-one correspondence between the elements in the sets. Therefore, if we were to take the set of natural numbers and set of odd numbers, we can say that they have the same cardinality because of that one-to-one correspondence between the two sets. The same could go for the set of natural numbers and the set of perfect squares. This can only be true because of the nature of infinite sets. We can see from this that natural numbers, integers, and rational numbers are all countably infinite.
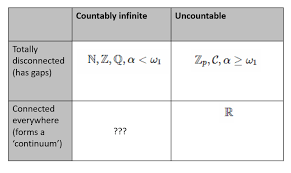
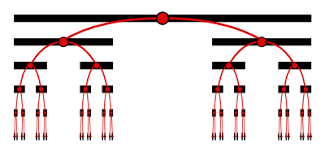
In regards to an uncountably infinite set, a few examples would be, “If A is a subset of B and A is uncountable, then so is B. This provides a more straightforward proof that the entire set of real numbers is uncountable. If A is uncountable and B is any set, then the union A U B is also uncountable. If A is uncountable and B is any set, then the Cartesian product A x B is also uncountable. If A is infinite (even countably infinite) then the power set of A is uncountable” (Taylor). Another example of an uncountably infinite subset would involve a decimal expansion. If we were to start with the closed interval [0,1], then if we remove the middle third of the set, we have [0,1/3] U [2/3,1]. Then we remove the middle third of each of the remaining pieces of the set giving us (1/9,2/9) while (7/9,8/9) is removed. If we were to continue, our set of points remaining after all the intervals are removed would not be an interval. Therefore, it would not be uncountably infinite. This specific example is called the Cantor Set.
As mentioned earlier, Cantor was big on the study of transfinite arithmetic. We will look into more detail about the study of transfinite numbers. “Since the time of Cantor, it has been the fashion to divide all arithmetic at the root into two separate branches: cardinal and ordinal. Each of these branches is supposed to have its peculiar operations of addition, multiplication, and exponentiation” (Birkhoff). When I think about the difference between ordinal arithmetic and cardinal arithmetic, ordinal arithmetic is mathematics that younger students study at an early age while cardinal arithmetic is what we have been discussing in this paper. In regards to the series of alephs and what was discussed earlier in the paper, these were used to describe higher orders of the term infinity. The first order of infinity, as we know, is denoted as ℵ0. This includes the set of whole numbers, set of integers, and set of algebraic numbers. This was a way to do arithmetic involving cardinality. When looking at ℵ1, it includes |R|=|(0,1)|=|P(N)|. In words, we say that it is cardinality of the "lowest" uncountably infinite sets. This can also be known as the cardinality of the continuum. Then for ℵ2=|P(R)|=|P(P(N))| it is the cardinality of the next uncountably infinite sets. So, what happens when we have ℵ0 +1? This would be the same as just adding 1 to a countably infinite set. There is no change to the actual size of the set since it is still countably infinite.