Infinity is a concept taught and used in many different mathematic subjects. The first idea of infinity being used in a daily mathematics situation is when we say something is approaching infinity; hence the idea of limits. For example, if we were to divide 1 with infinity, we physically wouldn’t know the answer to that question. In a math context, 1 divided by infinity is known as undefined. If we were to replace infinity with x, and increase the value of x, then we would see that 1 divided by x moves closer and closer to 0. We are not exactly sure what happens when x gets to infinity, but we know that 1 divided by x is headed towards 0. We are not allowed to say our answer is 0, so instead we say that the limit of 1 divided by x as x approaches infinity is 0. This is where the concept of limit plays its role. The word limit, in this sense, is the same as the word approaching.
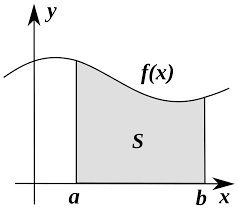
Another important application of infinity is relating it to the topic of integral calculus. Let’s use an example where we have a curve on a graph that is represented by y=f(x). Our question would be how can we find the area underneath the curve when also given a left bound (a) and right bound (b). Even with calculus, we could get a good approximation for this area. We can start by drawing out equal sections of rectangles in the area we want to find. Our next step would be to sum up the areas of each rectangle. We would say the area of each rectangle is f(xi)*delta(xi); and we would take the summation of all rectangles to give us an approximation of the area. As long as we were to use a finite number, we could get a better approximation by making our delta x smaller and even making more of our rectangles smaller. With our summation we are going from i=1 to i=n; therefore, resulting in delta x getting thinner and thinner, while n gets larger and larger. This all happens as n approaches infinity. Thus, this is our core idea of integral calculus. It is called this because the central operation being used is the integral from bound (a) to bound (b).
There are many controversies about infinity and how it may not seem to even exist and just be a part of our imaginations. Some believe that infinity cannot be logically consistent. In an article I studied, by Kip Sewell, he suggests that mathematicians should not use the word ‘infinity’, but resort to a more logically consistent alternative. He says, “that infinity is not coherent and ought to be dropped as a mathematical value, the question naturally arises as to how mathematics would then conceptualize unfathomably large quantities in calculation. An alternative concept to the traditional notion of infinity must be proposed. Such a concept is available to us called indefiniteness. Indefiniteness is not simply conceptual sleight-of-hand; it really is different from infinity in that it avoids the logical contradictions inherent in the notion of infinity but while still retaining the mathematical utility that infinity has (Sewell). He goes on to discuss how replacing this infinity with indefiniteness would make mathematics more logically consistent with it meaning it is greater than any computable value.
In an attempt to come full circle to how we started everything, it is clear to see that infinity has a huge role in mathematics. Not only in mathematics does infinity apply, but in other fields such as science, metaphysics, theology, and of course philosophy. Infinity can have a huge effect in our everyday lives. When thinking about how infinities actually have an effect on our lives, I think about this quote by Deepak Chopra which states, “You and I are essentially infinite choice-makers. In every moment of our existence, we are in that field of all possibilities where we have access to an infinity of choices.” I have never really thought about how many choices one individual is able to make in only one day. Not only does one person make countless decisions every day, but every one of those decisions has an effect on another person. In conjunction to adding numerous amounts of integers to get bigger and bigger numbers, the choices we make in our lives everyday whether big or small can quickly add up to a very large positive value. This motivates me to do my best to make the best choice possibly in any given circumstance.