Music
Modulations, or key changes, in a piece of music can sound natural or non-natural. Usually, anything that is only one note away will tend to sound natural.
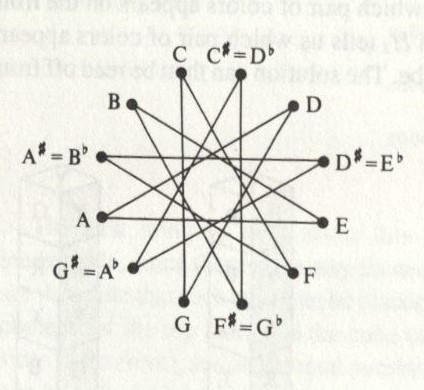
Any two keys that are obtained via a natural modulation are related. Thus, it seems natural to represent these relationships with a graph, where the vertices
are the various keys, and the edges are the related modulations between them (Wilson & Watkins, 1990)
. Below as an graph we get from natural modulations.
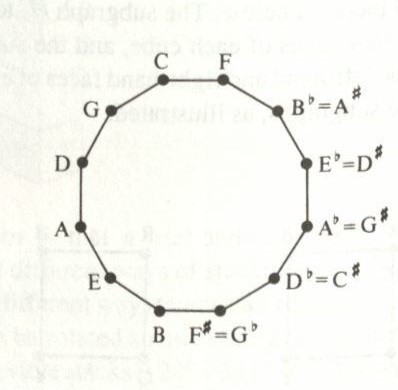
The above graph is arranged, so that the keys are listed in order from A to G. If we rearrange this graph, by getting rid of this arrangement, we end up with
the graph that looks like a cyclic C12.
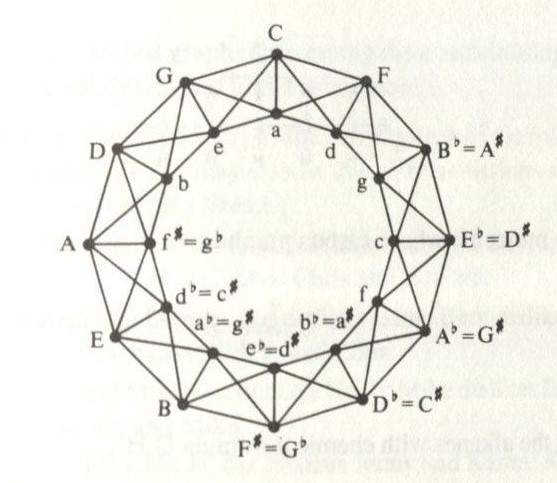
Note that all the above was done using major keys, if we include minor keys, things become more complicated, because many minor keys do not have natural modulations.
Although this is true, each major key is related to 5 different keys. The two keys related to the vertices on either side in the C12 graph, and the minors
that are associated with those three vertices. For instance, for C major, the 5 related keys are G major, F major, A minor, E minor, and D minor. If we combine this
all into one graph, we get the following graph, where major keys are capital letters, and minor keys are lower case letters.