Mathematics
Although, Graph Theory is a field of mathematics in and of itself, it also has applications to other areas of mathematics. Such as Algebra and Linear Algebra,
each of these areas help the study of graphs and are helped in return.
Algebra
The largest contributor to the study of graphs in algebra is the study of algebraic structures, specifically groups and group theory
(Biggs, Biggs, & Norman, 1993)
. Group theory is just the study of groups, and groups are any set of elements with a binary operator defined by
the following four axioms (Rowland & Weisstein)
.
1. Closure under multiplication
2. Multiplicative associativity
3. Identity element exists
4. Multiplicative inverse
When looking at graphs in the context of groups, we want to focus on automorphisms . Automorphisms are permutations of the graph's vertices which preserve
adjacency. They can also be thought of as the collection of permutation matrices that satisfy the multiplicative commutativity axiom with the adjacency matrix
(Beinke, Wilson, & Cameron 2004)
. For graph theory, this helps us to focus on symmetry. From automorphisms we can construct a hierarchy of
symmetry conditions, which we can use to investigate the consequences of these conditions. The consequences can tell us whether all the vertices are alike, whether
there is a bound to the level of symmetry, and what that bound would be.
In the field of Algebra, there are a lot of dealings with polynomials. A chromatic polynomial is a special polynomial and algebraic technique that counts the
colorings of a graph for coloring-type problems (Biggs, Biggs, & Norman, 1993)
. This can help us to find how many colors we need to complete
the coloring of any graph. But mostly the chromatic polynomial is used for its connection to subgraphs. The subgraphs are needed because they are used to find
the multiplicative expansions, which have very specifics restrictions. The multiplicative expansions that come from subgraphs are used to help us determine what
the chromatic polynomial is. This is extremely useful for large graphs.
Linear Algebra
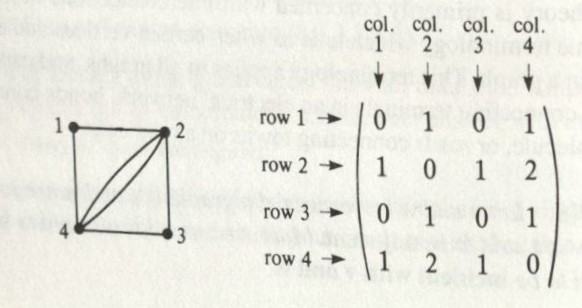
For Linear Algebra, the thing that graph theorist use most is an adjacency matrix and an incidence matrix. An adjacency matrix is defined as a nxn matrix
in which the entry in row i and column j is the number of edges joining the vertices i and j (Wilson & Watkins, 1990)
.
An example of a graph and its adjacency matrix can be found below.
An incidence matrix is defined as a nxm matrix in which the entry in row i and column j is 1 if vertex i is incident with edge
j, and 0 otherwise (Wilson & Watkins, 1990)
. Incident means that the vertex is connected to the edge or vice versa.
The incident matrix for the above graph can be found below. The graph has been relabeled with vertices in circles and edges as plain-text.
The other application of Linear Algebra that deals with adjacency matrices are eigenvalues and eigenvectors. If a graph is regular, then the eigenvalues of the graph's
adjacency matrix are bounded in absolute value by the degree of the graph (Biggs, Biggs, & Norman, 1993)
. The eigenvectors from the adjacency matrix
look more closely at the graph's geometry, specifically it's angles and star positions (Beinke, Wilson, & Cameron 2004)
.