Engineering

Architecture

There are many applications of graph theory in engineering. Here we will discuss a few of them

(Wilson & Watkins, 1990)

.
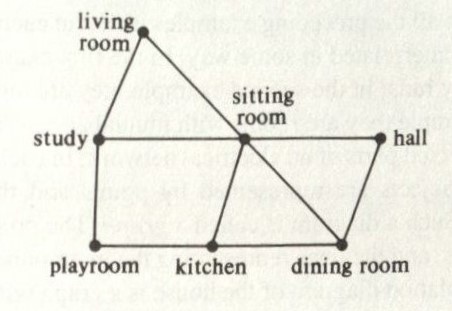
Architecture is one application. Suppose we design a house that looks like:

How can we make a graph out of this? If we consider the number of entrances (doors) into each room, we can get a graph that looks like:

This type of graph can help in large buildings, especially those that experience high foot traffic, i.e., where they are a lot of people passing through.

Structural Engineering

Thinking about how things are built leads us to talk about structural engineering. Structural engineering is focused on the design of building. Skyscrapers and other large buildings often rely on steel frameworks welded together. What happens if the frame built can't hold the weight?
Massive destruction.
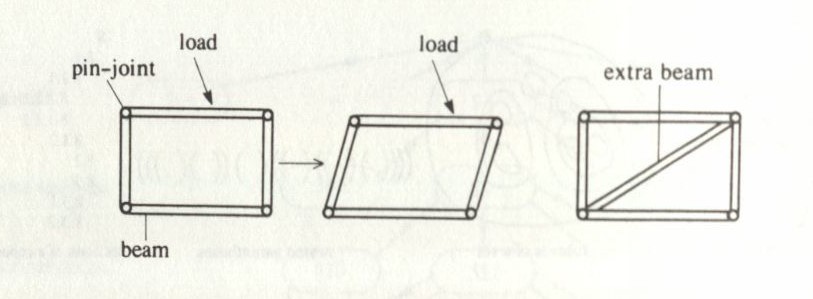
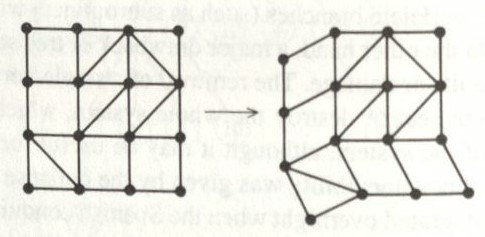
This is why they need to consider bracing the frameworks where the joints/vertices are pin-joints (they can swivel at the vertex). Here is an example of rectangular frame. Notice how it would move if we added weight to it, and what we would need to do to fix it.

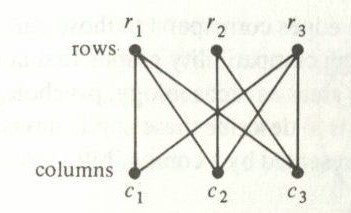
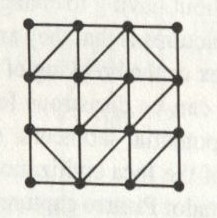
Each drawing of squares can be drawn as a bipartite graph, which is just a graph that has an even number of edges. What engineering gain from using graphs is the ability to answer the question, is it rigid? In other words, is frame overbraced? Consider the following drawing and its graph. Do you think it is rigid?

What about this one?

From these two graphs, we start to see a trend, disconnected graphs and connected graphs? Based on your observations, would you say that a rigid graph is connected and non-rigid graph is disconnected? If so, you are right! Connected graphs are considered rigid.
The idea of rigid graphs goes into an area of engineering and mathematics called optimal topology. Optimal topology studies the best possible solution (optimal solution) for material distribution

(Leary, Merli, Torti, Mazur, & Brandt, 2014)

. Basically, it studies the boundaries for an object by answering questions like, how much can an object carry, for how long, etc. It also considers loading conditions, stress (the physics kind), and any constraints

(Kaveh & Kalatjari, 2003)

Civil Engineering

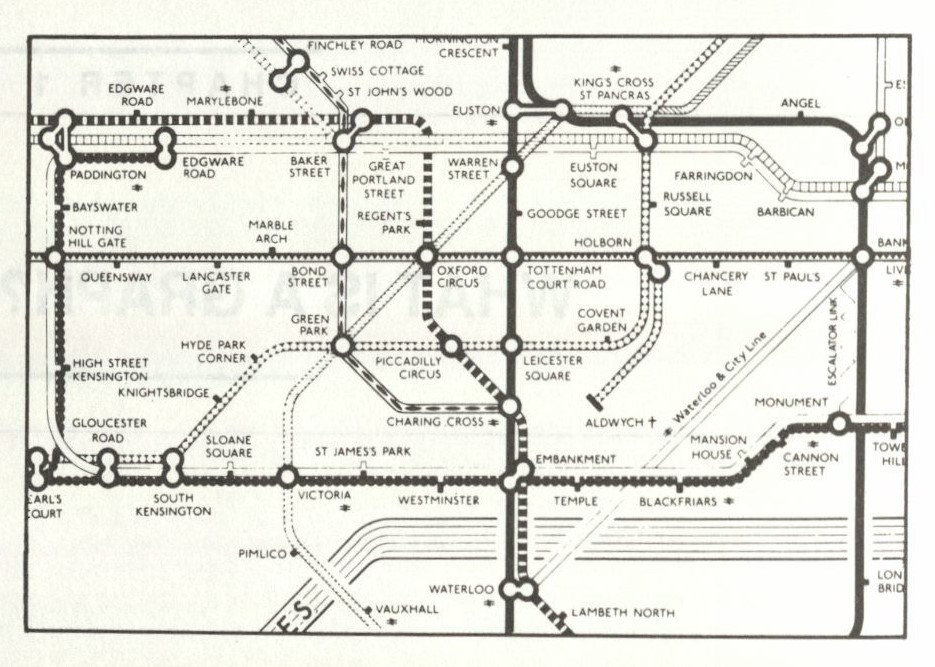
Civil engineers also do a lot with graphs and graph theory. Since they design roads, they need to think about traffic. Think about the London subway system.

There are lots of stations, but what passengers and thus engineers concern themselves with, is how to get from one station to the next. Thus, how are these stations or vertices connected, thus resulting in the need for graph theory.
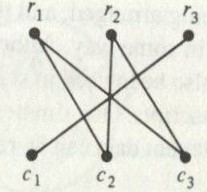
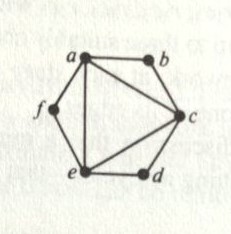
Not only is this true for subway systems, but also for roads. Now consider, a traffic light. A lot of crashes would happen if every car could proceed through the light at will. Civil engineers also concern themselves with timing the lights so that wait time is reduced and traffic keeps moving. They have to consider who can move at the same time without dangerous consequences, this is called compatibility. An example of a traffic light and its compatibility graph are shown below.

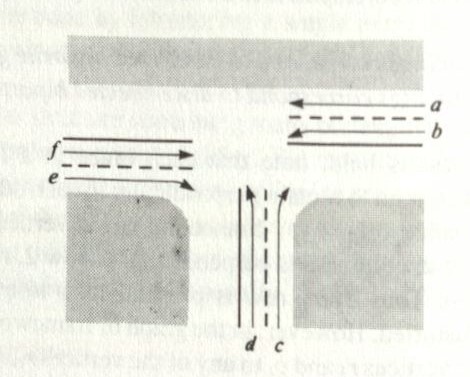
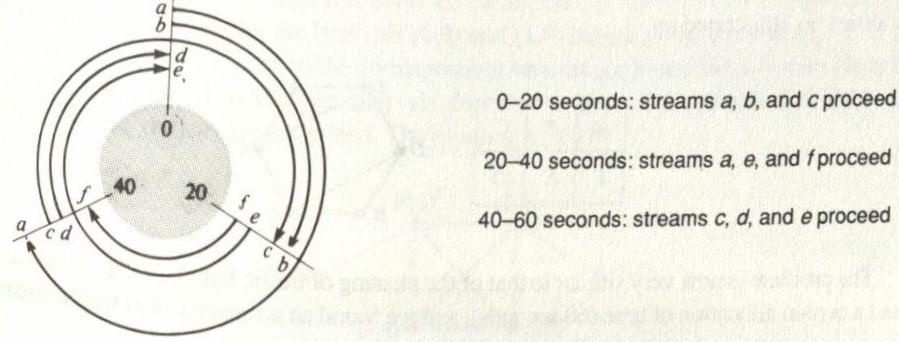
Thinking about wait times, engineers use a clock diagram, drawing compatible streams of traffic during the same time interval, switching and then drawing other compatible streams. Here is an example of what a clock diagram would look like for the traffic light above.