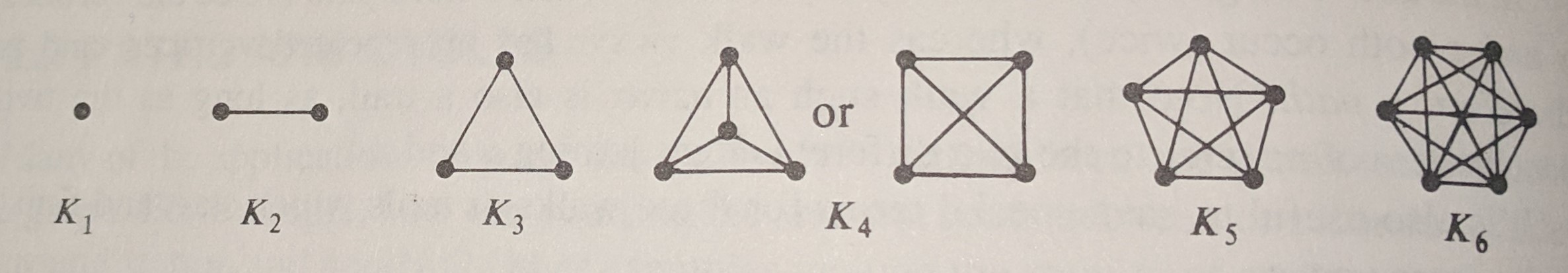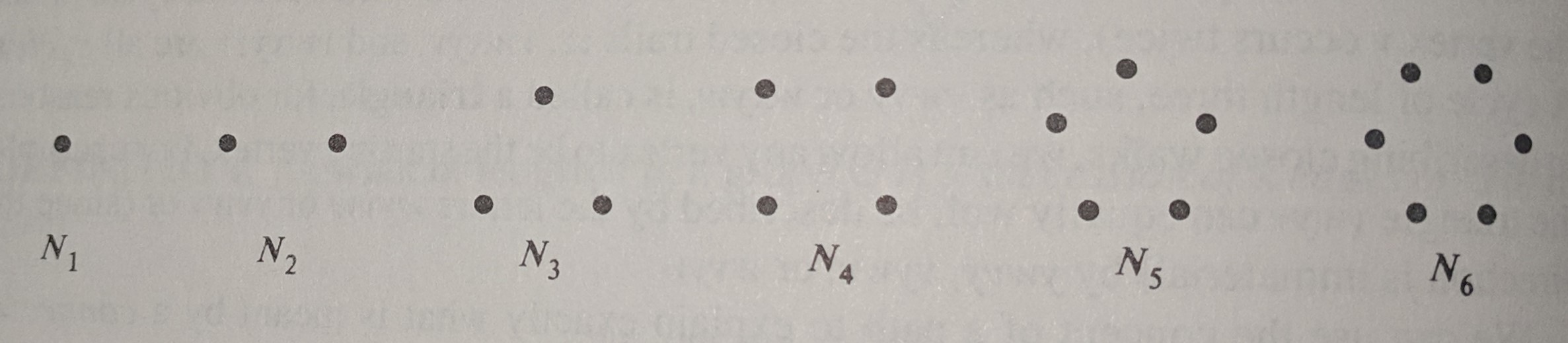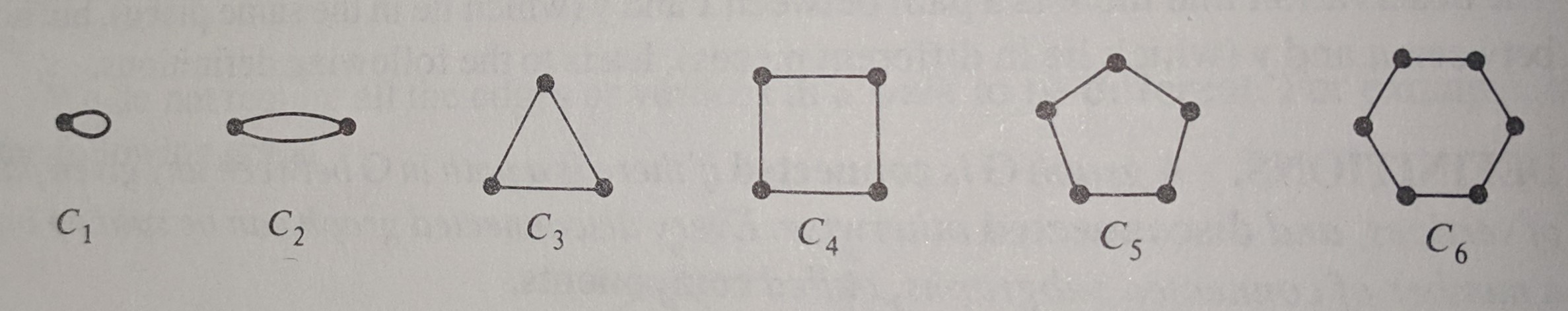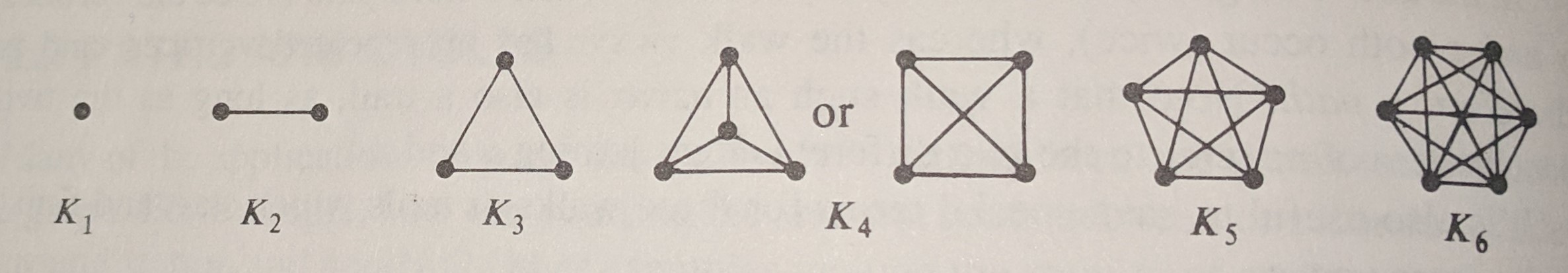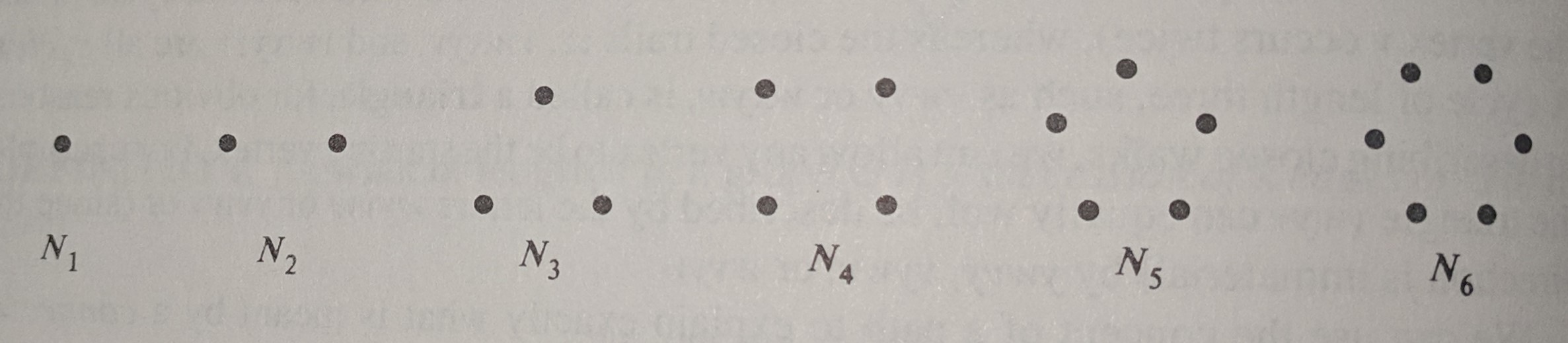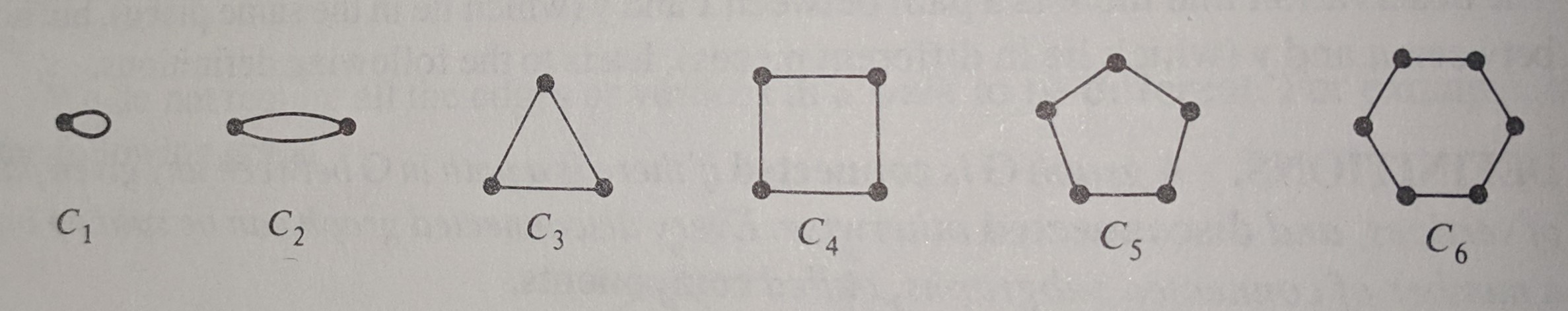Definition
In this section, we will examine some key definitions of graphs. Recall from the section "The Beginning" the definition that we gave in the podcast.
"Graph theory is defined as the mathematical structures of abstract relationships between objects (Andersen, 2011)
.
Of if you would like a more formal definition, it is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph
in the context of graph theory is made up of vertices, nodes, or points which are connected by edges, arcs, or lines (“Introduction to Graph Theory”, 2016)
.
This is why the notation for Graph Theory is written as capital g is equal to the ordered pair v comma e, where v represents the vertices of the graph, and e
represents the edges of the graph (G=(V,E))".
This is a very concise and effective definition. Wilson and Watkins (1990)
give the definition: A graph (G) consists of a non-empty set of elements, called
vertices (v) and a list of unordered pairs of these called edges (e). Any of these definitions will work for what a graph is. Some other key terms that we need to know are
presented in a table below. The key term (word) will appear on the left, with the definition on the right.
| Word |
Definition |
| Vertex-set |
The set of vertices of the graph, denoted V(G) |
| Edge-list |
List or set of edges of the graph, denoted E(G) |
| Multiple Edges |
Two or more edges connect the same two vertices |
| Loop |
An edge that connects a vertex to itself |
| Simple Graph |
Graph that does not have |
| Subgraph |
Graph where all vertices belong to V(G) and all edges belong to E(G), given a graph (G) with a vertex-set V(G) and edge-list E(G) |
| Degree |
the number of edges meeting at a given vertex, denoted by deg(v) |
| Adjacent |
Two vertices are joined by an edge |
| Incident |
An edge and a vertex connection |
| Walk |
The succession of edges from one vertex to the next |
| Trail |
All edges of a walk are different |
| Path |
All vertices of a trail are different |
| Closed Trail |
All edges of a walk are different |
| Cycle |
All trails and paths are different |
| Complete Graph |
Every two distinct vertices are joined by exactly one edge, denoted Kn, where n is the number of vertices |
| Null Graph |
A graph with no edges, denoted Nn, where n is the number of vertices |
| Cycle Graph |
A graph consisting of a single cycle, denoted Cn, where n is the number of vertices |
| Path Graph |
Graph that consists on a single path, denoted Pn, where n is the number of vertices |
| Bipartite Graph |
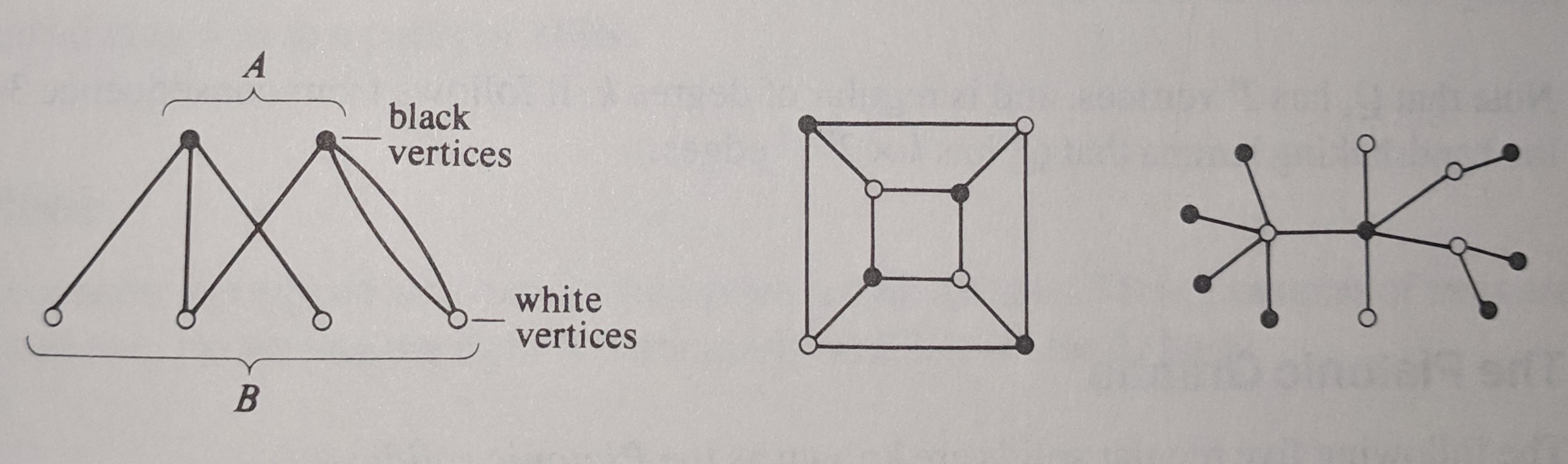
Graph whose vertex-set can be split into two sets A and B, such that each edges joins a vertex in set A to a vertex in set B |
| Tree |
Graph that contains no cycles |
| Spanning Tree |
Subgraph of a graph G that includes all the vertices of G and is also a tree |
|
| Branches |
Edges of a tree |
|
Here are a few examples of complete graphs, null graphs, cyclic graphs and bipartite graphs, in that order.
Notice that for complete graphs, we draw these are regular polygons. How we draw graphs is simply a matter of convention.