Properties of Pascal's Triangle

The fibonacci sequence is a recursion sequence created by adding the two previous numbers to make the next number, which gives {1,1,2,3,5,8,13,21,...}. This sequence can be found in Pascal's Triangle:

The square of the numbers in the second diagonal can be found by the addition of the number next to it and below it as such:

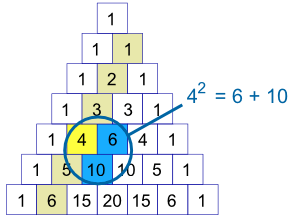
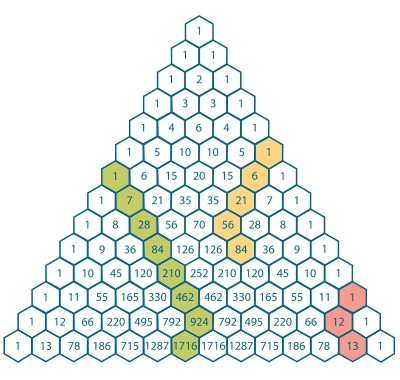
By selecting any diagonal and going down any amount of numbers, the sum of all those numbers is equal to the number below the last number in the diagonal, making a hockey stick shape.

Use the following applet to learn how Pascal's Triangle can be used to approximate e. S_n denotes the product of the nth row, where the top row denotes S₀. S_n-1denotes the product of the row above row n and S_n+1 denotes the product of the row beneath row n.
Lets consider the 3rd row. S_n is then S₃=1*3*3*1=9, S_n-1 is 1*2*1=2 and S_n+1=1*4*6*4*1=96. You can find the product of each row by typing in the multiplication of the terms in the nth row in the corresponding input bars. Thus, for S₃, you would type in the S_n input bar 1*3*3*1, by pressing enter it will then show the product is 9.

Start at S_n where n=1 and fill in the corresponding input bars to find what the ratio approaches as you move down Pascal's Triangle.