Pascal's triangle is made up of the coefficients of the Binomial Theorem which we learned that the sum of a row n is equal to 2n. So any probability
problem that has two equally possible outcomes can be solved using Pascal's Triangle. In the Problem of Points game explained in the video, the possible outcomes
were either heads or tails which both have a probability of .5. Thus, the total amount of different outcomes that could happen with a certain amount of coin flips
is 2n which we learned is equal to the sum of the coefficients in the nth row of Pascal's Triangle.
Let's consider the problem where we want to know the probability of flipping exactly 2 heads for 4 coin flips. We know how many total possibilities there are
for 4 coin flips by looking at the 4th row (when considering the top row the zero row).
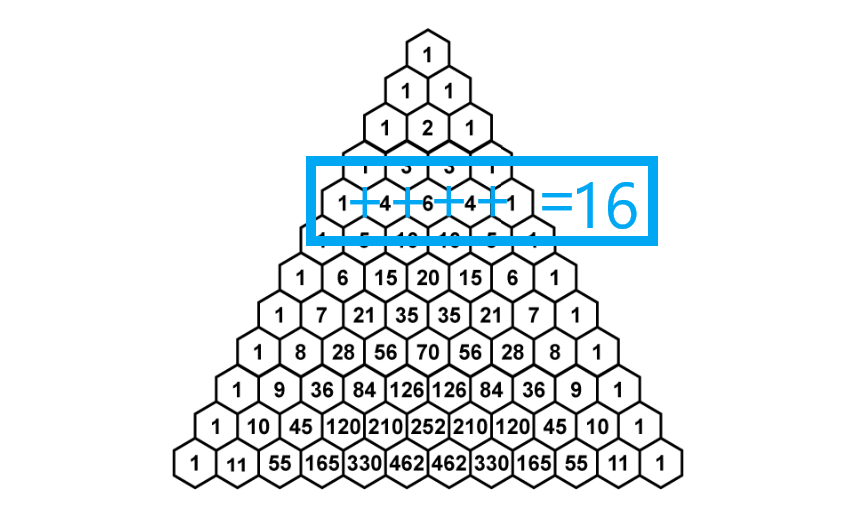
Thus, there are 1+4+6+4+1 = 24 = 16 possible different combinations
of heads and tails that can happen when flipping a coin 4 times. To then know how many possible ways there are to get exactly 2 heads, we know that the coefficients
of Pascal's triangle are all the coefficients of the Binomial Theorem which are combinations. Since we have four coin flips and are wanting to flip two heads,
the number of possible ways we can flip exactly 2 heads is 4C2=6, which is the third term of the 4th row of Pascal's Triangle. There is then a 6/16
chance of flipping exactly two heads when flipping a coin 4 times. If this problem had been at least two heads, you would then add all the terms of Pascal's
Triangle that came before the 6. In this case those terms are 4C0=1 which means there are 0 tails and 4 heads and 4C1=4
which is when there is 1 tail and 3 heads flipped. This would then give 11/16.
So, if you wanted to generalize this for any problem, you can find what the total number of possible outcomes there are for repeating an event that has two
equally likely outcomes n amount of times, by adding the terms of the nth row of Pascal's Triangle. You would then find what the amount of possible outcomes
there are for the event you are concerned with by looking at the term(s) of Pascal's Triangle that associates with the number that you are choosing from the total.
In the case with heads or tails, it is the number of heads you are wanting to choose from n amount of flips.