Have you ever heard of this effect? You might hear someone say that the flap of a butterfly's wings in Brazil can set off a tornado in Texas.

From 00:24-1:52
What did you hear Dr. Malcolm mention of the Butterfly Effect and Chaos? Butterfly Effect, Chaos, Unpredictability.
Listen to the podcast to hear how the Butterfly Effect was understood in the situation of weather.
**OPEN WITH MUSIC FOR 22 SECONDS. END MUSIC WITH FADE OUT**
<Hi, this is Ashley Bailey and welcome to my podcast. Today, my podcast is about Chaos Theory. Before I begin, let me explain an underlying concept. Isaac Newton is credited to nonlinearity or a system whose output does not vary in proportion to its input. For example, Newton puts on a 20-pound backpack. He does it fairly well. If we increase the weight of the backpack twice to 40 pounds, he has to work twice as hard. But if Newton adds one more pound to the backpack, he is unable to lift the backpack at all. This is nonlinearity. Now that we understand that, let’s look at a real historical situation.
**CUE THUNDER SOUND AT 1:12 FOR 5 SECS** **CUE BACKGROUND MUSIC AT 1:18 WITH FADE IN**
In the 50s and 60s, meteorologists worked to improve weather prediction. They understood the atmosphere is a fluid in motion and follows a version of Newton’s laws.
**CUE BACKGROUND MUSIC AT 1:24**
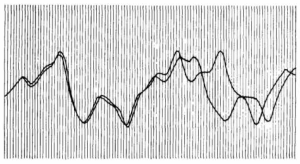
By gathering accurate data from all over the world, meteorologists hoped to use the past to predict the future. They hoped that a linear approximation would be good enough to predict the weather even though they knew there was some nonlinearity involved. Edward Lorenz, a mathematician and meteorologist, ran repeated runs of a computer simulation of weather. At one point, there was a run that he was interested in. Picking a point in the middle of the run, he gathered the data from that point, reentered the new data into his formula, and ran the program again. He then left for a coffee break and came back an hour later. When he came back, he found that the new run followed the old run for a couple of days in weather simulation. But after that, it didn’t follow the old program at all. He realized the computer computes up to 6 decimal places, but the new data he entered into the new run was 3 decimal places. The numbers were similar for a moment before the new data gave drastic new results over time.
This shows we are unable to predict the weather for more than 3 days ahead of time because we don’t have accurate data. Edward Lorenz called this the Butterfly Effect in his paper in 1972, saying that the flapping of a butterfly’s wings in one location could potentially affect the weather patterns in other locations. The Chaos Theory is sensitivity to initial conditions like we saw with the weather.
Consider Enrico Coen’s account of the human respiratory system:
“Our ability to breathe depends on the interplay between our nervous system, muscles, skeleton, and lungs. The function of our lungs depends on the composition of the mucus that lines its walls. The composition of the mucus depends on the proteins that transport negatively charged chloride ions. Changes in just one element of the integrated system can have disastrous consequences. Patients with cystic fibrosis have difficulty breathing because they carry a mutation in the gene needed for chloride transport. It only takes one change out of the three billion base pairs in our genome to cause the disease. The functioning of every individual depends on the integration of many different components”.
That’s all for today, and I hope to see you next time. Have a good one.
**END BACKGROUND MUSIC WITH FADE OUT AT 3:48** **CUE NEW MUSIC AT 3:53 FOR 3 SECS WITH FADE OUT**

As scientists were studying Chaos Theory, they looked into different systems that could become a chaotic system. One of those systems is the pendulum. The pendulum has been studied by Aristotle and Galileo to name a couple. Two nonlinearities that were disregarded by Galileo was: friction and air resistance. Galileo disregared them to get neat results for his research, but the nonlinearities were there. How does that relate to a chaotic system?
"Consider a playground swing. The swing accelerates on its way down, decelerates on its way up, all the while losing a bit of speed to friction. It gets a regular push-say, from some clockwork machine. All our intuition tells us that, no matter where the swing might start, the motion will eventually settle down to a regular back and forth pattern, with the swing coming to the same height each time. That can happen. Yet, odd as it seems, the motion can also turn erratic, first high, then low, never settling down to a steady state and never exactly repeating a pattern of swings that came before" (Gleick, 42).
Remind you of the unpredictability comment Dr. Malcolm made? Have a look at this applet with a double pendulum by clicking the button below. As you look at it, first explore the 'Sim' page that you are first brought to. Observe the double pendulum with a small amount of energy. Can you predict what it will do at a certain time?
Now using your mouse, drag one or both of the pendulums in a way that adds more energy to the system. Observe. Can you predict what the pendulum will do at a certain time?
Click on the 'Time Graph' tab near the top of the page. Now you see a graph for the movement of the top and bottom pendulums. Repeat the same process of observing the system with lower and higher energy. Can you predict what could occur next in a system with lower or higher energy?
How does this relate to what we know about weather? Does weather have a small amount of energy involved or a lot more than the energy you observed with a double pendulum? There is more energy involved in the complex system of weather, and it doesn't take a large change in initial conditions to change the outcome as we have been learning. Let's look at another pendulum scientists have used to better understand the challenge they have tried to solve.
"Another common pendulum toy is no more than a so-called spherical pendulum-a pendulum free to swing not just back and forth but in any direction. A few small magnets attract the metal bob, and when the pendulum stops, it will have been captured by one of them. The idea is to set the pendulum swinging and guess which magnet will win. Even with just three magnets placed in a triangle, the pendulum's motion cannot be predicted. It will swing back and forth between A and B for awhile, then switch to B and C, and then, just as it seems to be settling on C, jump back to A. Suppose a scientist systematically explores the behavior of this toy by making a map, as follows: Pick a staring point, hold the bob there and let go; color the point red, blue, or green, depending on which magnet ends up with the bob. What will the map look like" (Gleick, 43-44)?
Lets have a look.
This gives a visual representation at the end of the video of why meteorologists can't predict the weather more than a week in advance. The data they have, even now, is not precise enough to predict the weather accurately.
Note: The Podcast belongs to me, but applets and videos/pictures are credited to their orginal owners. I am using them for educational purposes only.