A Brief History of Infinity

The Greeks

          Some time between the fifth and sixth centuries B.C., the Greeks discovered infinity (Aczel, 2000) ¹ . The idea was so unnerving that to the philosophers and mathematicians who discovered it, the idea caused pain, insanity, and at least one murder. There is evidence to support that the idea of infinity originated with a haunting paradox attributed to the philosopher Zeno of Elea (495-435 B.C.). His most well known paradox was that of a race between Achilles, the fastest runner of Greek legends, and a tortoise. Since the tortoise is considered extremely slow, he is given a head start. Zeno's reasoning was that by the time Achilles had caught up to the place where the tortoise began, the tortoise would have advanced even further. By the time Achilles travels that new distance to the tortoise, the tortoise would have advanced further again. This pattern continues until the tortoise is moving an infintessimally small distance, but by the time Achilles gets to that point the tortoise would have advanced further on into infinity. Therefore, the fast Achilles never can beat the slow tortoise (Aczel, 2000) ¹ . Slow and steady wins the race, right? This paradox led to the idea that infinitely many steps can occasionally lead to a finite total distance.

          Although Zeno may have been the first philosopher to openly dable in the infinite, the real roots of infinity come almost a century earlier from the infamous mathematician, Pythagoras (569-500 B.C.) (Aczel, 2000) ¹ . Pythagoras was argueably the first mathematician to understand the importance of proving mathematical theorems. He discovered that a complete system of mathematics could be constructed where integers and their ratios were all that was needed to establish an entire system of logic and truth. Pythagoras built a beautiful world of mathematics and believed that numbers were created by God, therefore his system of mathematics was divine. One discovery brought his elegant mathematical world crashing down. It was the discovery of irrational numbers (Aczel, 2000) ¹ .
          Pythagoras shared his discovery of the irrational numbers with his group of followers, the Pythagoreans, but they were sworn secrecy because of the danger this finding brought. The discovery was made while examing the Pythagorean Theorem. Pythagoras found that in the case of a right triangle with legs both of length 1, the hypothenuse would have to equal the square root of 2. After observing this number, they realized that the square root of 2 could not be expressed at the ratio of two of God's creations. The cult believed that "God is number", therefore this finding jeopordized their entire belief system (Aczel, 2000) ¹ . Hippasus, one of the Pythagoreans, is believed to have committed the ultimate crime by informing the outside world of the existence of irrational numbers. Hippasus was expelled from the society for his crime, and it is rummored that Pythagoras himself strangled or drowned the traitor, while another story claimed that he was set accross on a boat that was later sunk by the Pythagoreans (Aczel, 2000) ¹ . The Pythagoreans idea of divinity sunk with Hippasus, but out of the ashes was born the concept of the continuum.
          Later, Eudoxus (408-355 B.C.) and Archimedes (287-212 B.C.) used the Pythagoreans discovery to experiment with infintessimally small numbers. They used the idea of dividing the area of a figure into very small rectangles and then summing their areas to approximate the area of the figure. This was a great application of the concept of a potential infinity whose limit is finite, but no one dared dable in the continuum.

          It took over 1300 years before a new discovery was made pertaining to actual infinity. Galileo Galilei (1564-1642) began examining geometry and how circles related to polygons. He determine that as you increase the sides of a regular polygon, the figure will eventually look almost like a circle. Galileo concludes that if a regular polygon were to have infinte sides, then it would be a circle (Aczel, 2000) ¹ . He later expanded his understanding of sets and cardinality by applying the logic of infinity. It is defined that two sets have the same cardinality if there is a one to one relation between the sets. When observing finite sets it is easy to determine if they have the same cardinality or not; all one has to do is count the number of elements and see if the sets have the same number of elements. Galileo began wondering if he could apply this idea to functions. By setting up a one to one correspondence between the set of natural number and the set of all of their squares, Galileo determined that the number of elements in the natural numbers is the same size as the number of elements in the set of its squares. This seems counterintuitive because it is obvious to see that there are many elements in the natural numbers that are not in the set of its squares. However, Galileo realized that when dealing with infinity, 2 sets of apparently different size can be made to have the same number of elements. Galileo was the first person in history to have touched actual infinity and survived the ordeal. Unfortunately,only a few years later in 1642, Galileo died (Aczel, 2000) ¹ .

          In 1817, Bolzano finally entered uncountable infinity. He found a function that was continuous but not differentiable. This same discovery would be made decades later by Weierstrass who would initially get all of the credit for the discovery. What Bolzano did was look at the function y=2x. He allowed the function to act on the domain space of real numbers between 0 and 1. This produces a range of 0 to 2 in the real numbers. Bolzano concluded that since every real number between 0 and 1 was assigned a value, this meant that there were as many numbers between 0 and 1 as there are between 0 and 2 (Aczel, 2000) ¹ . Later this idea lead to what is now called the Bolzano-Weierstrass property. A space is said to have this property if every infinite sequence in a subset of the space has a limit point within the space. This suggests that infinite sequences in a bounded space contain limit points.

          Bernhard Riemann (1826-1866) gazed deeper into the infinite in several ways. He generalized the metric of the Pythagoreans to a more complex space. Riemann examined Euclid's theory of space to discover what is now called the Riemann sphere (Aczel, 2000) ¹ .
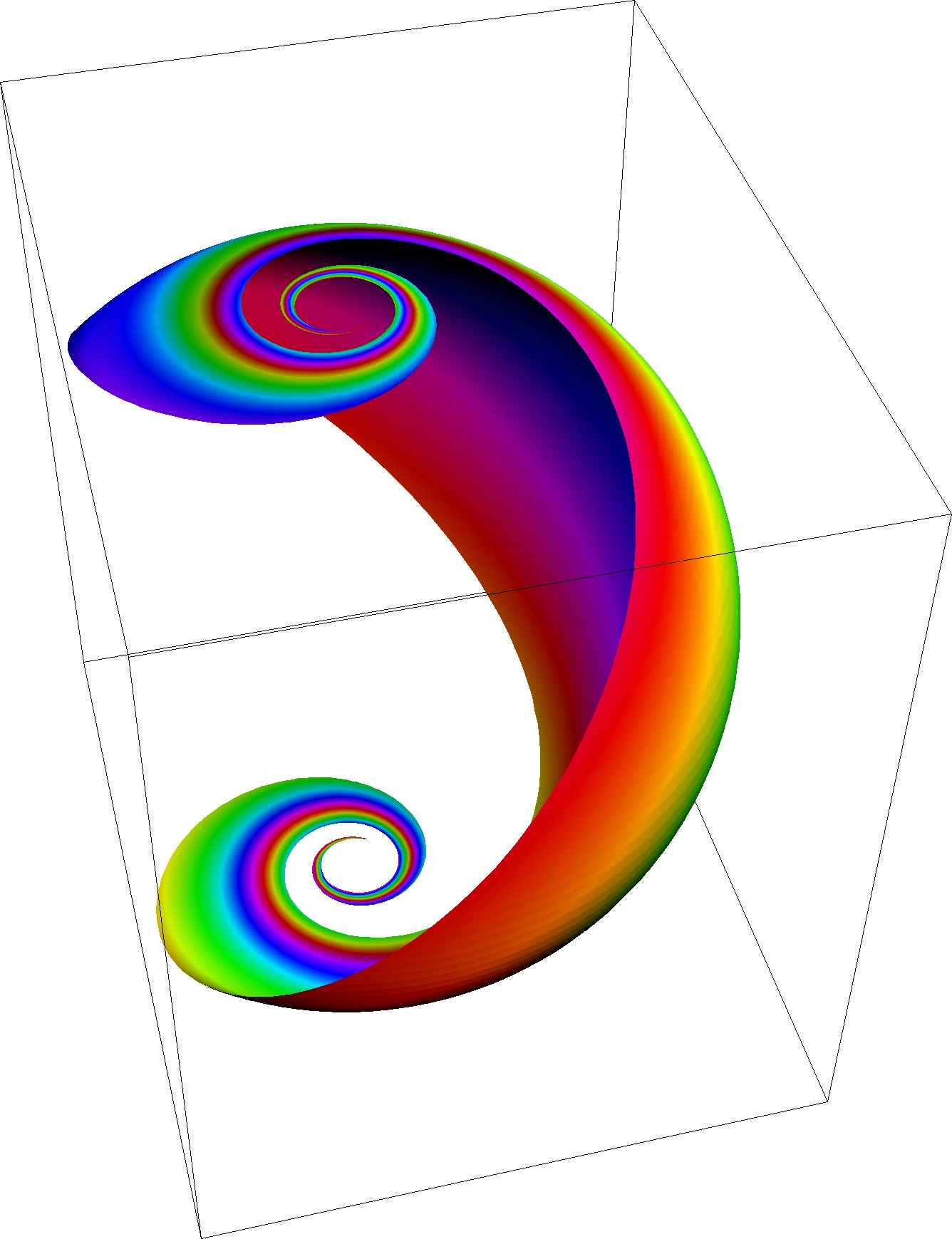
The sphere shows how infinity can be made compact by adding a "point at infinity" to the sphere. On the sphere the north pole is the point at infinity to which all lines and points on the pane tend as we go infinitely far in any direction in the plane. This makes the plane become compact, which suggests that it is closed and bounded.
          Another contribution of Riemann is through calculus. The Riemann Integral of calculus is defined as an infinite sum of integrals of step functions. These infinite sums later became the starting point of study of the infinite for Georg Cantor (Aczel, 2000) ¹ .

          Georg Cantor received his doctorate in mathematics in 1869 from the University of Berlin. When he graduated he was offered a teaching position at Friedrich’s University in Halle, 70 miles southwest of Berlin. Cantor was excelling in his profession but in 1884 he was struck with depression. After recovering from his illness, he wrote in a letter that just before his mental breakdown he had been working on the “continuum hypothesis.” He bounced back and forth from being well and falling ill again until he died in the beginning of 1918 (Aczel, 2000) ¹ .
          The hypothesis is that 2 ^{ℵ ₀} =ℵ ₁ where ℵ ₀ represents the smallest infinity, countable infinity, and ℵ ₁ represents the infinity just larger than that, an uncountable infinity, which Cantor referred to as the absolute. Through transfinite arithmetic, a branch of mathematics discovered by Cantor, and set theory, Cantor belived by exponentiation, one a function involving countable infinity could become uncountable. Unfortunately, he was neither able to prove or disprove his hypothesis although he tried for years. The continuum hypothesis has continued to be one of the most enduring mysteries in mathematics and remains a mystery today (Aczel, 2000) ¹ .
          Many believe that he was driven mad by the continuum problem and it is true that before every episode of depression he was studying this problem. However, there is evidence to support that he suffered from bipolar disorder and manic depression which are much more likely to have caused his death (Aczel, 2000) ¹ .


Click on the side link to explanation of mathematics to learn more about transfinite arithmetic and other facinating phenomena involving infinity.

Back to Top