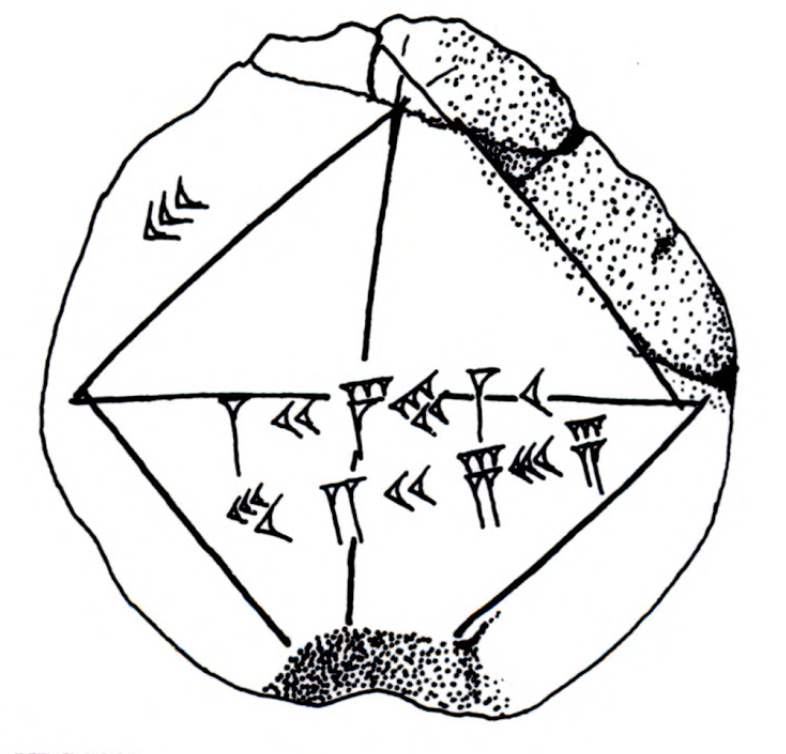
Moving forward we gained more knowledge about the Babylonians and we found that they had a symbol that represented the number 30. If we wrote this number in our base-10 system, we would get 1+24/60+51/60²+10/60³=1.414213, which is the decimal value of the √2, accurate to the nearest one hundred thousandth! And if you take this number and multiply it by 30, we get 42.426389, which is the sexagesimal number 42;25;35-the number on the second line below the diagnol in the picture above. With this information it is undeniable that the Babylonians knew the relation between the length of the diagonal of a square and its side, d=a√2 (Maor). So, in return they were familiar with the Pythagorean Theorem or at least with its special case for the diagonal of a square (d²=a²+a²=2a²) more than a thousand years before Pythagoras named it!

There are two things about the tablet shown above that are worth mentioning. First, it proves that the Babylonians knew how to compute the square root of a number to a remarkable accuracy, as close to the capability of a modern eight-digit calulator, and second it showed an example of how to find the diagnol of any square by simply multiplying the lenght of the side by 1;24;51;10. Most individuals would follow the obvious and more tedious route: start with 30, square it, double the result, and take the square root: d=√30²+30²=√1800=42.4264 (Maor). Imagine if you had to do that over and over again, not cool. Instead, we can follow the anonymous scribe who carved these numbers into a clay tablet nearly four thousand years ago and just multiply the side of the square by the √2.

Now, you have all heard of the pythagorean triples, right? Well so did the Babylonians. How did they know about them, especially such enormously large ones like (4601,4800,6649)? The only logical explanation is that they had to know the algorithm which, 1,500 years later, would be formalized in Euclid's Elements: Let u and v be any two postive integers, with u>v; then the three numbers a=2uv, b=u²-v², c=u²+v² form a Pythagorean triple (Kadison). It is required that u and v are of opposite parity-one even and the other odd. And that they do not have any common factor other than 1, then (a,b,c) is a primitive Pythagorean triple. Meaning that a, b, and c have no common factor other than 1. It isn't hard to confirm that the numbers a, b, and c, as given by the below equations, satsify the equation a²+b²=c².

Now, let's look at another historical group that may have beat Pythagoras to the punch line but didn't get the glory. They are the Egyptians! The Egyptians have also used a lot of mathematics, obviously because of their pyramids, but we can't find any real proof of the Pythagorean Theorem. It is thought that they used a²+b²=c² to build their pyramids, but they have never expressed it as a useful theory. Even with that as a let down, we will still visit their area of expertise and relate what we know to how they thought. Now the Babylonians recorded all of their work on clay tablets, but the Egytptians used papyrus. Papyrus is a highly fragile medium and were it not for the dry desert climate, their writings would have been long gone. We still don't have a lot of knowledge about the Egyptians and it is less extensive than that of its Mesopotamian contemporary, but we do have artifacts that come from the burial sites of the ruling Egyptian dynasties, a handful of surviving papyrus scrolls, and hieroglyphic inscriptions on their temples and monuments (Maor).

With all of these artifacts not once is there any reference to the Pythagorean theorem, either directly or by implication. One concept that does appear repeatedly is the slope of the side of a pyramid, a question of considerable significance to the builders, who had to ensure that all four faces maintained an equal and uniform slope. But still, no Pythagorean theorem, which to me is weird. Of course, just because something doesn't seem to exist and can't be found, doesn't mean that it was never there. But, unfortunately the Rhind Papyrus represented a summary of the kind of mathematics an architect might use in his career, and the absence of any sign of the Pythagorean theorem is a high indicator that the Egyptians simply did not know it (Kadison). Often it is known that they used a rope with knots tied at equal intervals to measure distances. The 3-4-5 knotted rope was a common occurrence, so maybe they knew about the 3-4-5 triangle with a 90 degree angle leading to the fact that 3²+4²=5² (Maor). But that has no evidence to support it. They may have not even used the 3-4-5 knotted rope to create a 90-degree angle.

Some day archeologists may unearth a document that shows a square with the lengths of its side and diagonal inscribed next to them, but until that happens, we cannot conclude that the Egyptians knew of the relation between the sides and the hypotenuse of a right triangle.

We've taken a moment to look into who may have or may have not discovered the Pythagorean Theorem, so now let's look at the history and the background of the guy who owns the title and why he owns the title. Pythagoras.

Pythagoras's first major scientific discovery was in an acoustics, not a very common subject if you ask me. As the story goes, while walking down a street one day he heard sonorous sounds coming from a blacksmith's shop. Stopping to investigate, he found out that the sound originated from the vibrations of metal sheets hit by the blacksmith's hammer: the larger the sheet, the lower the pitch of the sound it produced (Kadison). Pythagoras then experimented with bells and water-filled glasses and found the same general relationship: the more massive an object, the lower the pitch of its sound. However, Pythagoras was not content with a small almost insignificant relationship. His next move was to study and investigate the vibrations of strings. He ended up discovering that the pitch of their sound is inversely proportional to their length. For example, imagine two strings that were identical in thickness and material as well as held under the same tension, with different lengths. If one string was as twice as long as the other, then the shorter string will vibrate at twice the frequency of the long string. This means the strings are an octave apart in musical terms.

Similary, if you have a length ratio of 3:2, it will correspond to an interval of a fifth, and a ratio of 4:3 will correspond to a fourth, and so on and so forth. The names "octave," "fifth," and "fourth" come from the position of these intervals in the musical scale. This discovery marked the beginning of mathematical physics, making it very important and being known as the first time a natural phenomenon was described in terms of a precise quantitative expression. This was only the beginning of Pythagoras's discoveries and all it took was one step more to his next. He soon found out that if the two strings are allowed to vibrate at the same time, they will produce a musical chord. Pythagoras was delighted as he continued to explore and as he did he found that simple ratios of string lengths produce pleasant chords, or consonants (Veljan). Among the are the intervals just mentioned: the octave, fifth, and fourth, which Pythagoras called the "perfect intervals." If a ratio was more complicated it was less pleasing. For example, the ratio 9:8 produces a second, a distinctly dissonant chord. Pythagoras concluded that numerical ratios, rule the laws of musical harmony, or in other words, the entire universe. It became the Pythagoreans cornerstone of their world picture. Everything must be perfect in their eyes. So, the Pythagoreans decided that if numbers govern the laws of musical harmony, then they must also govern everything else in the universe (Maor).

Since the Pythagoreans were so fixed on their idea of numbers, they ran into a few problems. Such as the advancement of science. On the other hand, it helped them study the mathematical properties of numbers. They mainly studied the positive integers which would later grow into the modern number theory (Veljan). They may have been a little too obsessed with numbers, blinding them from other truths that may have better explained the workings of nature. By subjugating the laws of nature to the Greek ideals of beauty, perfection, symmetry, and harmony, the Pythagoreans hindered the progress of the physical sciences for a good two thousand years. Nevertheless, the Greek world picture was to dominate astronomy for over two thousand years. It was completely unacceptable if someone were to thinkg that the heavenly bodies traveled in anyting but a circle, it had to be perfect, no exceptions. Even when Nicolaus Copernicus, dethroned the Earth from its lofty position at the center of the universe and replaced it by the Sun, he still held onto the good old circlular orbits. Johannes Kepler was the first to put circular orbits to rest and replace them with ellipses in 1609 (Maor). Newton later expanded Kepler's ideas to include parabolas and hyperbolas.

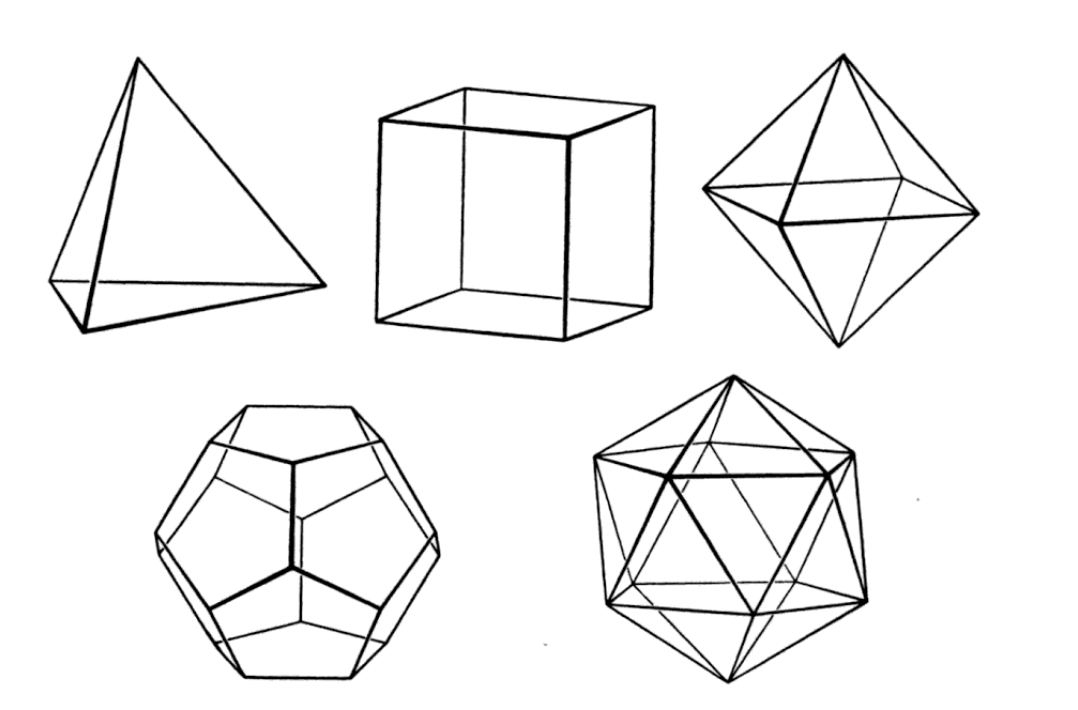
Let's return to mathematics. As it was known the study of numbers became a spirtual quest, something akin to the modern Kaballah. They believed that every number carried a symbolic identity. The number one was the generator of all numbers, because every number can be created from it by repeated addition. The numbers two and three stood for the female and male characters, respectively, and five, for their union (Veljan). Five was also the number of regular polyhedra, solids whose faces are identical regular polygons as seen below. The tetrahedral, the cube, the octahedron, the dodecahedron, and the icosahedron represented the five elements of which the universe was thought to be made: fire, earth, air, water, and the heavenly dome surrounding them (Maor). Dealing with the number 5 formed the idea of the pentagram and it became the Pythagorean emblem.

Just to add more emphasis to how much the Greek's loved perfection, let's take a look at their idea of perfect numbers. Notice that the proper divisors of 6 are 1, 2, and 3, and since 1+2+3=6, six is the first perfect number. The next three are 28(=1+2+4+7+14), 496(=1+2+4+8+16+31+62+124+248), and 8,128(=1+2+4+8+16+32+64+127+254+508+1,016+2,032+4,064). These four were the only perfect numbers known to the Greeks. The fifth perfect number 33,550,336, was only found in 1456. Currently there are 43 perfect numbers that are known to exist and all of them are even. We are still unsure if any odd perfect numbers exist, nor whether the number of perfect numbers is finite or infinite.

So, we've seen how much the Greek's and Pythagoras loved perfection. Right? Well, we've made it to the point where Pythagoras began working on the so called Pythagorean theorem that we've been getting at this whole time and he discovered something he probably wished he hadn't. It is thought that he was working on the 45-45-90-degree triangle and naturally that gave them a problem: given a square of unit side, find the length of its diagonal. Denoting this length by d and using the Pythagorean theorem, we have d²=1²+1²=2, so that d=√2. They ran into a problem, thinking what kind of number is √2? Therefore, he found a number that cannot be written as a ratio of two integers, or in other words an irrational number (Veljan). Neither the proof nor details of the discovery have survived, so all we can do is rely on writings by later authors and add our own spectulations. Euclid did some work but it was beyond Pythagoras's time. So we'll just fall back on the facts that lead us to believe that Pythagoras was the first to prove a special case of a right isosceles triangle, that is, a 45-45-90-degree triangle. The thoughts that led to irrational numbers is shown below.

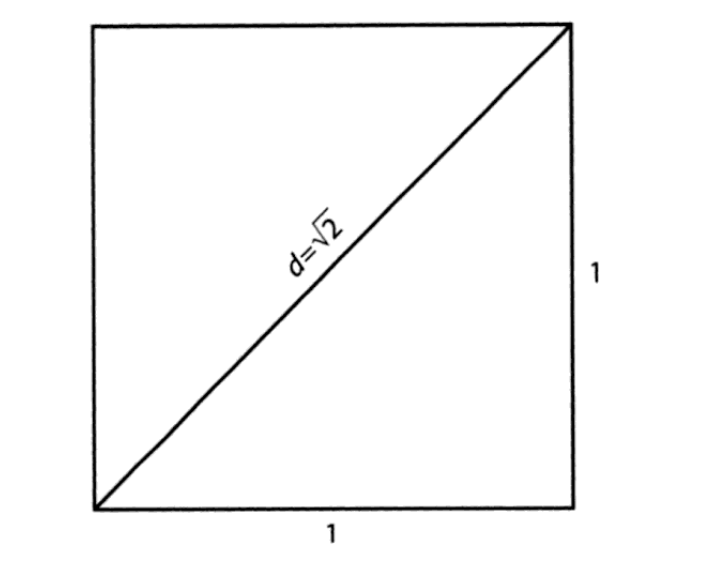
This proof was already known to the Hindus and Pythagoras may have heard of it during his travels around the Mediterranean (Maor). The question you may have is, did Pythagoras also prove the general case? There is no direct evidence, but it wouldn't be hard to believe if he did. We do have evidence from the Chinese of their accomplishments. By viewing the image below, you can see that by tilting the inner square from its 45-degree position, we get the configuration that follows. Square ABCD is now dissected into an inner square KLMN and four congruent right triangles. By reassembling these right triangles, we see that the remaining area is the sum of the areas of squares 1 and 2, that is, the squares built on the sides of each of the right triangles. It has been believed that the Chinese beat Pythagoras to the punch line.

Focusing back on the discovery irrational numbers, we saw that the Greek's went balistic. They even started killing anyone who believed it to be true (Veljan). Pythagoras tried to keep it a secret for as long as possible to save others' lives. In fact a guy of the name Hippasus wanted to reveal the discovery to the world and ended up getting thrown overboard into the sea. His body rests to this day at the bottom of the Mediterranean (Maor).

We've looked at groups who orginated the thought of the Pythagorean theorem, we've looked at groups who may or may not have known about the theorem and we've learned about how everything came to be. The Pythagorean legacy lasted well over two thousand years, and to some degree continues to the present. This legacy and obsession of the Pythagorean discoveries dealing with number symbolism and number mysticism, influenced countless writers, artists, and thinkers. The relations between mathematics and music, first discovered by Pythagoras, had repercussions in Renaissance Europe, where cathedrals were designed according to the musical proportions 2:1, 3:2, and 4:3 (Imhausen). They thought and pictured God's hand in any musical scale. Renaissance scientists were inspired by the phrase "music of spheres." Everything is perfect. The astronomer, Johannes Kepler (1570-1631) was one of the last Pythagoreans. Kepler spent a good 30 years of his life seeking to discover the laws of planetary motion in musical harmony. Kepler believed that each planet plays a certain tune according to its distance from the Sun. If a planet was closer to the sun, then it had higher notes. As mentioned before, it was Kepler who strayed away from the old Greek circular orbits (Imhausen). He discovered ellipse paths, setting modern astronomy on its course.

This Pythagorean philosophy lingers on today in the shadows of mathematics. At the beginning of Einstein's general theory of relativity, the idea that simplicity and symmetry play a role in the laws of nature once again was discussed.

"It's more important to have beauty in one's equations than to have them fit experiment." -Paul A. M. Dirac

A Pythagorean school was even organized (Imhausen). It acquired the reputation of an exclusive, aristocratic club. In today's vocabulary, we would say an elitist group. It wasn't long before the members were harassed, ridiculed, and tortured. Pythagoras himself was forced to flee or was killed. His exact death is unknown but findings suggest he lived to be around 80. Meanwhile, the ancient world was changing and the Persian Empire was rising to prominence and soon replaced Babylon as the dominant power east of the Mediterranean. There was a time of peace where Pericles, Socrates, Anazagoras, Zeno, and Parmenides made Athens their home (Imhausen). Then there was a war and everything was a disaster. After time Athens slowly regained its leading role. Plato came to be and established a healthy democracy. He wasn't a mathematician himself but he stongly believed in logical thinking and learning in general.

As for Pythagoras, almost nothing is known about his life; even his year and place of birth are uncertain, but it seems likely he was raised and educated in Athens (Maor). He loved mathematics and contributed to many discoveries.

Fun facts about the Pythagorean theorem:

The Pythagorean theorem is known to be "dazzinlgy beautiful." A theorem beautiful? That seems interesting to me, but it's true. In 2004, the journal Physics World asked readers to nominate the twenty most beautiful equations in science. The top winner was Euler's formula, followed in order by Maxwell's four electromagnetic field equations, Newton's second law of motion F=ma, and a²+b²=c², the Pythagorean theorem. It was only fourth place. Note that the contest was for the most beautiful equations, not the laws or theorems they represent. Of course how can you judge beauty of a theorem, I guess that depends on what qualifies it to be beautiful in a mathmatician's eyes.

~The most recent challenge~

Fermat tried to go a step further than a²+b²=c² and find integer solutions of the equations x³+y³=z³, x⁴+y⁴=z⁴, and so on. None were ever found. Fermat thought he had a proof that no integer solutions of the equation xⁿ+yⁿ=zⁿ exist for any value of n greater than 2 (Imhausen).

"To divide a cube into two cubes, a fourth power, or in general any power whatever into two powers of the same denomination above the second is impossible. I have found an admirable proof of this, but the margin is too narrow to contain it." -Fermat 350 years pass by and numerous mathematicians try to reconstruct Fermat's "admirable proof," but all of them failed. Leonhard Euler (1707-1783) in 1753 proved Fermat's claim for the special case n=3. Other special cases followed, and with the help of computers, all cases for n under 100,000 have been proven, but of course, that isn't the same as proving it for all values of n. It remained unresolved and become known as Fermat's Last theorem (Kadison).

Acomplishments of Pythagoras: he contributed to the mathematical theory of music, he was a musician, he noticed that vibrating strings produce harmonious tones when the ratios of the lengths of the strings are whole numbers, and that these ratios could be used in other instruments as well, he proved that the sum of the angles of a triangle is equal to 2 right angles, or 180 degrees, in astronomy, he taught that the Earth was a sphere at the center of the universe, he also taught the orbit of the Moon was inclined to the equator, and that he discovered irrational numbers. It is interesting that he discovered irrational numbers because Pythagoras believed the philosophy that all things are numbers, so the fact that a number which could not be expressed as a ration of two whole numbers did not sit well with him (Kadison). In fact, the general religion of the Greeks at the time supported the idea that nature is mathematics and the more one learned about mathematics, the closer one got to understanding God. Since God is perfect, all numbers were believed to be perfect. Irrational numbers would not sit well with any Greek, so the Pythagoreans became a secret society. In fact, legend has it that the Brotherhood drowned a man at sea for trying to announce the discovery of irrational numbers. Top