

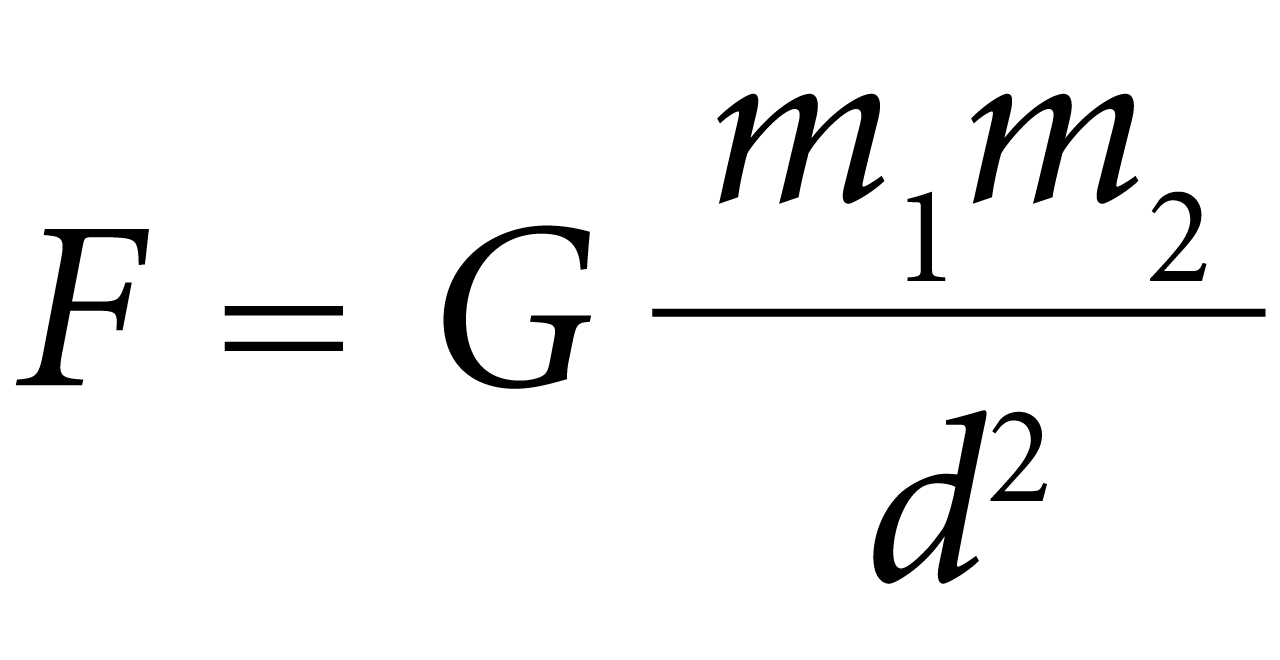
This equation can be applied to the relation between three bodies as such:
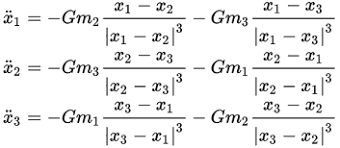
This is system of second order differential equations where G is the gravitational constant, m n represents mass of body n, and x represents distance from centers of mass between the bodies. In physics, the dot above the dependent variable is an indication of a derivative changing in time. In other words, these equations model the movement of three bodies- each of which is impacting the forces acting on each of the other masses as they move through space where that force is inversely proportional to the square of the distance between two centers of mass.
Below is a computer modeling of the three body problem in which all masses are equal. For even more information regarding the mathematics of the problem, click the "I" at the top of the window.
While we can used computer models to evaluate the equations numerically (and create the simulation above), centuries of searching for an analytic solution by mathematicians proved fruitless. In 1887 Heinrich Bruns and Poincare would finally put the matter to rest but not by presenting a solution. They, instead, went about proving that the three body problem had no analytic solution and, except for special cases, the trajectories of the bodies would be non-repeating.
While this perplexing problem had all the attributes of what would become known as a chaotic system, the mathematics community of the time ended its exploration of the matter at this point. It wouldn’t be till much later that a connection between this and many other mathematical and real world phenomenon would be connected.