Where is the Golden Ratio found in nature, art, and architecture?
Nature:
Logarithmic spirals can be seen on many plants, such as the seed patterns of flowers, the leaves of some succulents, and the outside of pineapples. Count the number of spirals clockwise and counterclockwise, and they will be consequetive fibonacci numbers. Divide the larger by the smaller and the ratio is close to the Golden ratio. The Universe is conjectured to expand in a logarithmic spiral. Natural phenomena such as hurricanes spiral logarithmically as well.
Art:
Leonardo Da Vinci created many works in accordance with the Divine Proportion, including the Mona Lisa, the Last Supper, The Divine Proportion (a sketch of a man outlining the golden ratio in his proportions), and illustrations of platonic solids. Also, today, many cartoons are created based on this ratio.
Architecture:
Many famous buildings are conjectured to have been built with the Golden Ratio in mind. However, it is important to keep in mind that just because the ratio can be found in the structure, does not prove that the intent to build it such a way came from the Golden Ratio. Examples of these buildings are the Great Pyramid of Giza, the Parnthenon, Notre Dame, the Taj Mahal, and Toronto’s CN Tower.

How does the Golden Ratio relate to five-fold symmetry?
Using only one type of regular polygons, with which polygon(s) can you fill space without any gaps such that it is symmetric?
Up to six sides, the answer is triangles, cubes, and hexagons. Up until the 1970s, 5 fold symmetry was thought and even proved completely impossible.
However, Roger Penrose in the 1970s proved that 5 fold symmetry is actually possible! And it depends on the Golden Ratio!

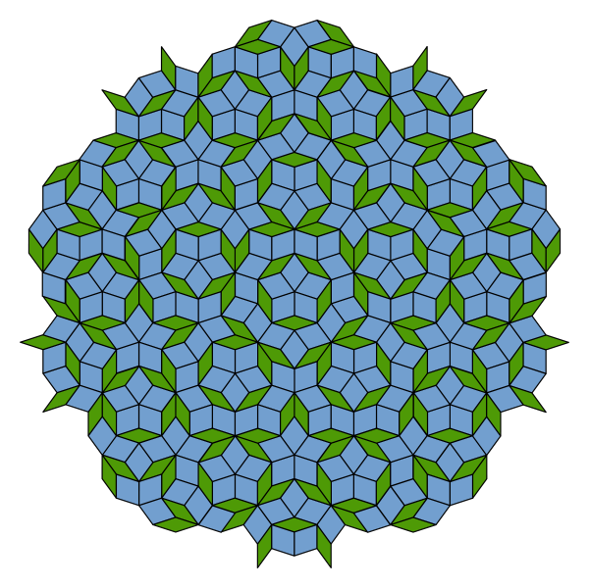
He recognized that it could be done by using shapes pulled from the Pentagram inscribed in a regular Pentagon. These golden shapes he arranged to form Penrose tiles.
With these tiles, he realized that if they were arranged in a non-repeating manner, such that it is asymmetrical, the tiling would exhibit instances of five-fold symmetry. This tiling is today called Penrose tiling. Penrose tiling can follow a fractal generator and so combine a neverending pattern with five-fold symmetry all dependent on Phi!

In 2011, it was discovered, and awarded with a Nobel Prize, that 5 fold symmetry occurs naturally on the atomic level with a shape known as the quasi-crystal. Below is a cross-section of a quasi crystal whose subatomic parts interact based on relations of phi in non-repeating patterns with five-fold symmetry.

With which Platonic Solids is the Golden Ratio evident?

The tetrahedron, cube, and octahedron have integer coordinates for the vertices. However, this is not true for the icosahedron and dodecahedron! Both of these platonic solids have golden rectangles inscribed inside. Below are diagrams of the three golden rectangles inside of each of the platonic solids along with the coordinates of the vertices.


For more sacred solids based on phi, see Sacred Solids
"Geometry has two great treasures: one is the Theorem of Pythagoras; the other, the division of a line into extreme and mean ratio. The first we may compare to a measure of gold; the second we may name a precious jewel. "
Johannes Kepler, (1571-1630)
Johannes Kepler, (1571-1630)