The Golden Ratio, Φ, is an irrational number equivalent to (1+ √ 5 )/2 which is approximately 1.61803399.

Euclid in about 300 BC defines it as: "A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the less."

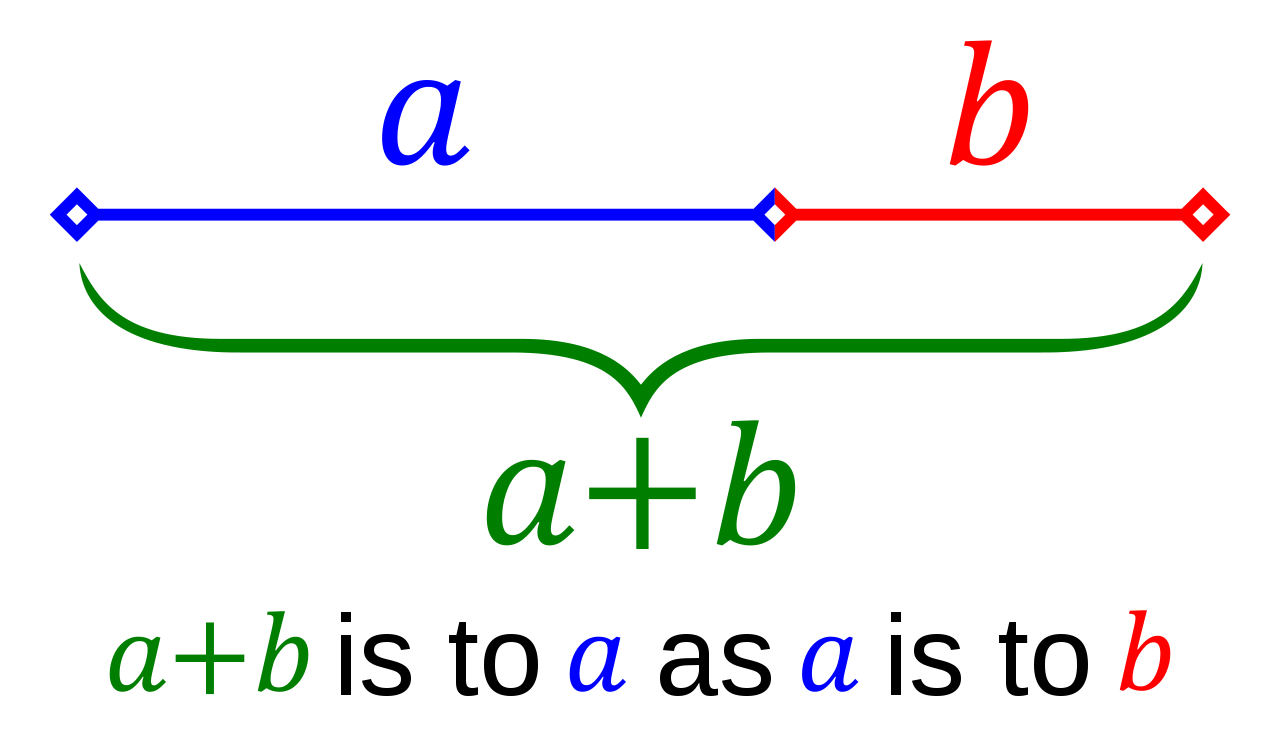
Or in simpler words, with the diagram below it means that a segment is cut in such a way that (a+b) divided by a is the same ratio as a divided by b.

I created the video below to describe the relationship. It shows how dividing consequetive fibonacci numbers results in a number that converges to Phi, the further the fibonacci numbers are in the sequence.

The following applet in desmos also shows how the ratio of consequetive fibonacci numbers converges to around 1.618:

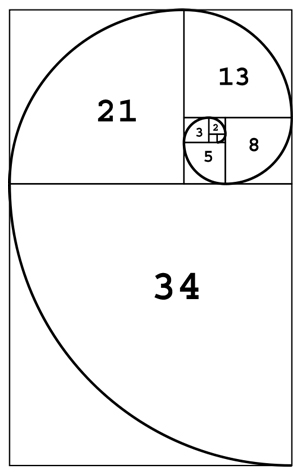
Golden rectangles are rectangles such that the ratio of the length and the width is equal to the golden ratio. In the diagram below, when squares with lengths corresponding to the fibonacci numbers are placed counterclockwise in sucession, the rectangles created increasingly have side lengths whose ratios converge to the Golden ratio. Mario Livio (2002) states that " if you connect the successive points where these ' whirling squares ' divide the sides in Golden Ratios, you obtain a logarithmic spiral that coils inward toward the pole (the point given by the intersection of the diagonals ... which was called fancifully ' the eye of God ' )."

Golden triangles are isosceles triangles such that the congruent sides have a length that is phi times the base. Below, with this original Geogebra applet, I have shown 3 things.

1. Check the box labeled How do we know triangle ABC is a golden triangle?. The measure of segment DC is equivalent to the measures of segment AB and segment AC added together, because as the circle shows with radius A, that AD is congruent to AC. Then looking at AD/DC we see that it is equivalent to AC/AB.

2. Check the box labeled Show the Logarithmic Spiral. This shows how not only can a logarithmic spiral be created by 'whirling squares', but also by golden triangles repeatedly inscribed inside one another, cutting the sides in golden ratios.

3. Check the box labeled Mathematical Proof. Golden triangles have angle measures 72, 72, and 36 degrees. This proof uses the angle degrees to prove that ABC is indeed golden.