Explanation of Mathematics
The Math behind the Harmonic Series
The harmonic series in mathematics is a divergent series that is produced by the summation of 1 over n as n goes to infinity:
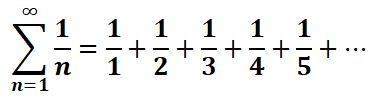
String Lengths and Consonance
Like was said in the section entitled "Historical Information," Pythagoras observed that when you have two strings of the same width and tension, but different lengths, they will either sound consonant (good) or dissonant (bad) when played together. The harmonic series models a relationship of string lengths and helps us find consonant sounding strings.
A string of length a will vibrate at a frequency of f when played.

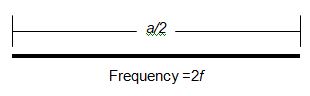
If a string of length of a/2 is played it will vibrate at a frequency of 2f.
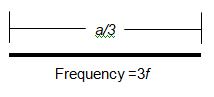
Similarly, if a string of length a/3 is played, it will vibrate at a frequency of 3f.
This goes on and on creating a series of strings that when played together sound consonant (Gibson) 3 .
Standing Waves
The harmonic series not only models what string lengths sound consonant together, but it also describes how a string vibrates over its entirety.
Let me explain, when a string is plucked it will vibrate over the whole length of the string. At the same time the "string... vibrates over fractional divisions of its length
(1/2, 1/3, 1/4, 1/5, 1/6, etc.) producing a series of harmonics (overtones) whose frequencies are inversely proportional (2x, 3x, 4x, 5x, 6x, etc., where x is the fundamental frequency of the string)
to those fractional divisions. Theoretically an infinite number of these multiple modes of vibration exist, each mode producing its own harmonic. As one ascends the series, the amplitude, or loudness
of each harmonic tends to diminish, so the higher modes produce harmonics that are usually too soft for us to hear" (Bain, p.3) 1 . In other words, when a string is plucked,
it vibrates over its entire length, which is 1, and produces a fundamental tone. This tone is the loudest and the one you tend to hear. However, at the same time, the same
string also divides itself into two equal parts, 1/2, and they vibrate at the same frequency which is twice that of the fundamental frequency. This frequency is not as loud as
that of the fundamental, but your brain still picks up on it. At the same time, the string also divides itself into three equal parts, 1/3, and they vibrate at the same frequency
which is three times that of the fundamental. This frequency is even softer than that of the 2nd harmonic, but your brain will still pick up on it. The string keeps dividing itself
in this harmonic pattern over and over again creating an unending amount of frequencies. Since they get softer and softer they eventually become negligible to the ear.
This relationship is modeled in the applet below. It starts out with the fundamental frequency or the first harmonic. This is the string vibrating
over its entirety (thus the solid line is showing the string, and the dotted line shows its oscillation). The points where the amplitude of the wave is at its lowest, in this
case the ends of the string, are called nodes and are represented by the two dark gray points. The points where the amplitude of the wave it at its highest, in this case
the maximum and minimum height of the string, are called antinodes. Explore the applet by selecting different harmonics and their nodes. What do you recognize about the different
harmonics? How are they the same and different? How many nodes and antinodes are there compared to the number of harmonics it is? Do some harmonics share nodes with other harmonics?
To see what Standing Waves would look like in real life, check out this video 2 .
Overtones/Harmonics, Tomato/Tamato
When a string is plucked, it plays all of these frequencies together. Like was said before the fundamental frequency is the
loudest and is the sound we associate with the note being played. All the other frequencies are called overtones or harmonics as we have been calling them,
and can be heard ever so faintly. Since we can calculate these overtones using the harmonic series it is sometimes referred to as the Overtone Series
(Bain, p.1) 1 . These overtones are very important and are what give the instrument being played
its timbre which we will talk about later.
Science behind Consonance
With all this talk of consonant and dissonant sounds, one might ask who was the person who decided for all man-kind what sounds
good and what doesn't? There have been many studies conducted trying to figure out what sounds "good", what sounds "bad", and surprisingly, most people
would answer with similar results, even across all nations. In The Frontiers in Neuroscience journal there was an article published entitled
"The Harmonic Organization of Auditory Cortex" by Xianoqin Wang 9 . In the article it states how the harmonic series is...
"a fundamental structure of sounds encountered in the natural environment... Harmonicity is an essential component
of music found in all cultures. It is also a unique feature of vocal communication sounds such as human speech and animal vocalizations. Harmonics in sounds
are produced by a variety of acoustic generators and reflectors in the natural environment, including vocal apparatuses of humans and animal species as well
as music instruments of many types. We live in an acoustic world full of harmonicity. Given the widespread existence of the harmonicity in many aspects of the
hearing environment, it is natural to expect that it be reflected in the evolution and development of the auditory systems of both humans and animals, in
particular the auditory cortex. Recent neuroimaging and neurophysiology experiments have identified regions of non-primary auditory cortex in humans and
non-human primates that have selective responses to harmonic pitches. Accumulating evidence has also shown that neurons in many regions of the auditory cortex
exhibit characteristic responses to harmonically related frequencies beyond the range of pitch. Together, these findings suggest that a fundamental
organizational principle of auditory cortex is based on the harmonicity. Such an organization likely plays an important role in music processing by the
brain"(Wang) 9 .
The same laws that built nature also built us, so it makes sense that a law of nature like the harmonic series would also somehow be imbedded into our own brains as a way of understanding the world around us.
<-- Previous to Historical Information
Next to Significance of Applications -->