In algebraic terms, The Pythagorean Theorem is as follows: a^2+b^2=c^2, where c is the hypotenuse and a and b are the legs of a right triangle. This theorem has been proven multiple times. For example, in the book, The Pythagorean Proposition, written by an early 20th century professor, Elisha Scott Loomis, over 367 proofs of The Pythagorean Theorem were collected and written out in this book. Technically speaking, the number of proofs would be limitless because of the number of different geometric shapes that can be used to prove the theorem.

Many of the proofs of The Pythagorean Theorem stemmed from Euclid. Euclid, like Pythagoras, was a Greek mathematician that lived around 300 BC. He is often referred to as the father of geometry. Euclid helped discover many of the different relationships that exist amongst geometric shapes. He used many of these relationships and geometric shapes to help prove The Pythagorean Theorem. Because of this, he is credited for discovering many of The Pythagorean Theorem proofs.
One of the proofs from Euclid is included here verbatim from Euclid V1.31 in translation by Sir Thomas L. Heath. This proof is taken from www.cut-the-knot.org.
In right-angled triangles the figure on the side subtending the right angle is equal to the similar and similarly described figures on the sides containing the right angle.
Let ABC be a right-angled triangle having the angle BAC right; I say that the figure on BC is equal to the similar and similarly described figures on BA, AC.
Let AD be drawn perpendicular. Then since, in the right-angled triangle ABC, AD has been drawn from the right angle at A perpendicular to the base BC, the triangles ABD, ADC adjoining the perpendicular are similar both to the whole ABC and to one another [VI.8].
And, since ABC is similar to ABD, therefore, as CB is to BA so is AB to BD [VI.Def.1].
And, since three straight lines are proportional, as the first is to the third, so is the figure on the first to the similar and similarly described figure on the second [VI.19]. Therefore, as CB is to BD, so is the figure on CB to the similar and similarly described figure on BA.
For the same reason also, as BC is to CD, so is the figure on BC to that on CA; so that, in addition, as BC is to BD, DC, so is the figure on BC to the similar and similarly described figures on BA, AC.
But BC is equal to BD, DC; therefore the figure on BC is also equal to the similar and similarly described figures on BA, AC.
Therefore etc. Q.E.D.

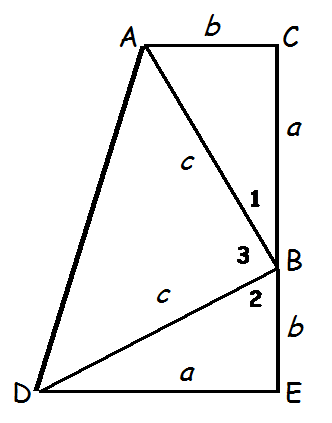
You may be surprised to find that one of our very own presidents developed a roof of The Pythagorean Theorem. Can you guess which one? It was President J.A. Garfield back in 1876. He showed that by using the trapezoid ACED he could prove The Pythagorean Theorem. First, he took the trapezoid and divided it into two right triangles and one isosceles triangle, as shown below. He then found the area of all three triangles. The area of the three triangles came out to be ab+(1/2)c^2. This is equal to the area of the trapezoid which is (1/2)*(a^2+2ab+c^2). Once the two areas are set equal to each other and simplified, the equation will reduce to a^2+b^2=c^2. President Garfield was born in a log cabin and raised on a farm. This goes to show you don't have to be a mathematician to prove The Pythagorean Theorem. The proof above was taken from www.cut-the-knot.org.
The Pythagorean Theorem is crucial in deriving one aspect of Euclid's Geometry. The theorem serves as a basis for the distance between two points. Euclid was able to show that given any two points in space, the distance between those two points will equal the square root of the sum of the squares of the differences in the x and y coordinates of the two points. In other words, the distance formula. If you would like to see a formal derivation, follow this LINK and prepare to be amazed.
Now you have seen just a few of the many proofs of The Pythagorean Theorem. Because of the simplicity of its derivation, anyone with the will and desire can sit down and come up with a proof of this theorem. If you would like to see more proofs, I highly recommend THIS site. Enjoy : )