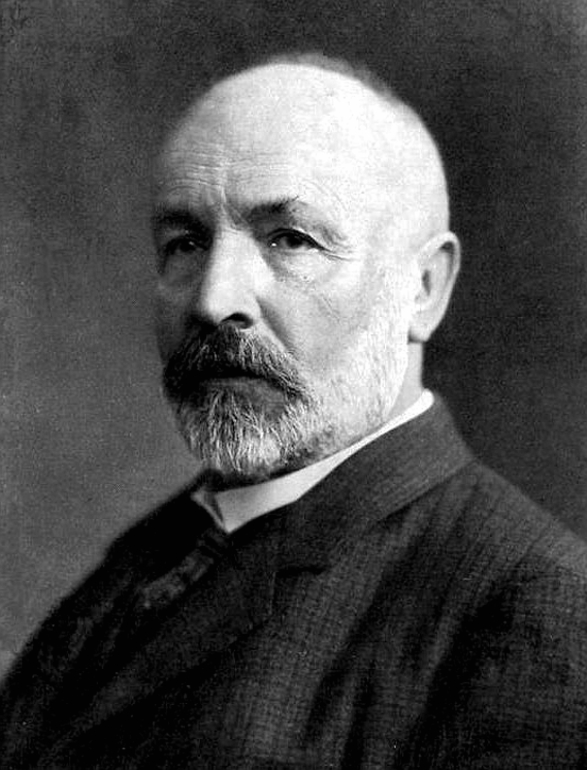The History of Set Theory
The history of set theory cannot be discussed without the mention of Georg Cantor's name, the forefather of this foundational mathematical concept and the man shown in the photo above. Although his name is widely associated with the conept, he was not the first to conceive of the idea. However, the practice of organizing information into sets is such a natural process for the human mind that there is no distinct "emergence" period where set theory was first introduced. Evidence of the use of sets can be traced back to the 3rd Century C.E. with the Tree of Porphyry and its use of classifications in a hierarchy of groups.
The complexity of the set theory related to mathematics began to emerge with the slow acceptance and consideration of infinity. Reconsidering Leibniz's thoughts on the infinite, three 19th century German figures led the way of accepting infinite in mathematics and the building of set theory, promoting the study prior to Cantor's use. These three are Bolzano, Riemann, and Dedekind.
Bolzano's contributions weren't as influential as the other's, but his initial work was fully supportive of the infinite. His work published in 1851 argued that paradoxes considering infinity are logically harmless - a contrary idea to what was previously thought. In his attempt to prove the existence of infinite sets, Bolzano unknowingly touched on the idea of set cardinality while attempting to prove one-to-one mappings, but never made the definite discovery.
Similarly to ideas of Bolzano, Riemann's view on mathematics and the concept of topology held propositions of basing all of mathematics on the idea of sets and groupings. Additionally, Riemann played a leading role in the support of conceptual mathematics and complex analysis - both of which influenced Dedekind and Cantor and their development of set theory. This time period, of the beginning influences of Riemann, Dedekind and Cantor, is the closest thing there is to an explicit emergence time frame of set theory.
These dates are from 1868 to 1872, which included Dedekind's publishing of Riemann's work of the Riemann integral that catalyzed working with real analysis in mathematics. An additional stepping stone for Dedekind took place in 1871, pertaining to his work with algebraic numbers. Working within a field of algebraic numbers, Dedekind was considering a ring of integers and defined "ideals" as a particular subset of the ring he was working in and proceeded to perform operations on this subset. This initial work of giving subsets precise definitions and performing operations on them is relatable to many of the twentieth century works on other sets, providing evidence of how significant this step was in the development of set theory.
In 1872, Dedekind and Cantor each provided definitions for the set R of real numbers and expounded on its structure and properties. Both built their definitions from the starting point of rational numbers as elements and studied the topology of R from there. Later in 1873, after much progression in the field, Cantor made a discovery that altered people's ways of thinking and introduced several new properties sets could hold. Dedekind deduced a proof that showed the set of all algebraic numbers held a one-to-one correspondence with the natural numbers, making it a countably infinite set. Similarly, Galileo introduced a paradox that showed the set of all squared natural numbers is countably infinite as well and applied his findings to line segments of different lengths. Cantor took these findings and questioned if such a mapping existed between the natural numbers and the real numbers. Starting with the assumption that a one-to-one mapping exists between these two sets and using a diagonal proof, Cantor disproved the existence of this mapping and therefore showed the set of real numbers to be uncountable. This showed that there are more elements in the set of real numbers than there are in the set of natural numbers, which provided evidence and support to Galileo's earlier paradox.
This discovery was groundbreaking, and the emergence and use of set theory only grew from there. From 1878 to 1885 Cantor published several pieces of work that helped with the integration of set theory into a regular used branch of mathematics. Cantor defined different notation, axioms, and properties; he heavily studied abstract set theory, the topology of specific sets, and order typed sets. All of his work, along with others, led to the rise in the study of pure mathematics during the late nineteenth century. Moving past their previous focuses, Cantor, Dedekind and their colleagues directed their interests to the study of pure mathematics. This change of focus led to deeper understandings of sets' characteristics and different theorems and axioms, such as the Axiom of Choice and The Well-Ordering Principle. Consequently, along with gaining a deeper understanding from a more rigorous studying of the pure mathematical side of set theory, Cantor and a few other mathematicians uncovered a few paradoxes in the logistics of set theory, which held them back from making progress for a significant amount of time.
Although many mathematicians directed their focus to the pure mathematical side of set theory, this wasn't the case for all mathematicians' interest with the new concept. In 1897 at the first International Congress of Mathematicians, keynote speeches focused on the importance of set theory in analysis. A few years later, mathematicians Borel, Blaire, and Lebesgue studied Cantor's previous work with the set of real numbers further in what they called descriptive set theory. A descriptive set is a definable set of real numbers, and the reason for its focus of study is to uncover its structural properties. The first of these sets to be studied were the Borel sets, which led to the study of Blaire functions and different properties such as the property of a set being Lebesgue measurable. The study of descriptive sets was not an easy one; in fact one mathematician came to the conclusion in a published paper that "one does not know, and one will never know" in reference to one particular set's properties. It wasn't until the 1940's that mathematician Godel discovered where the difficulties came from and in turn decided there was a need for new axioms.
This axiomatic and structural approach to set theoretic mathematics continued in its development throughout the 20th century, advancing several branches of mathematics and recognizing others as their own branch. Beginning from Cantor's proof that the set of real numbers is larger than the set of natural numbers, set theory was commonly considered in conjunction with the study of logic; but today we can see today that set theory is integrated through all branches of mathematics and its axiomatic structure can be credited with the rise of modern mathematics (Ferreirós).
For the dates and history of the emergence of the notation commonly associated with set theory, click this | link | .