Fractals have been around for as long as the earth has been in existence because they exist everywhere in nature. But it was only fairly recently that substantial discoveries were made in the mathematics and significance of fractals.

The first person we know of to publish anything about Fractals was Gaston Julia (1873-1978) around the time of World War I. When he was only 25 years old, he studied and discovered the underlying concepts of fractals and published his ideas. He became well known for it among the mathematics community, but for unknown reasons he and his work dropped out of the mathematical community and was not heard of again until Benoit Mandelbrot found and studied his work (Wertenberger).

Benoit Mandelbrot received his Ph.D. in mathematics and worked at IBM with a crew of nonconformist thinkers. They were trying to solve a problem with transmitting computer data over telephone lines and information was not getting through. As he graphed the noise data he found that it had a self-similar property to it. This reminded him of some of the concepts he read about Fractals from Julia's work. Using his access to advanced computers and technology that Julia never had, Mandelbrot was able to produce millions of iterations of Julia's equations, graphed them and found the Julia set fractals (Jersey & Schwarz, 2011).

Mandelbrot then coined the term "Fractals" based on the Latin verb "frangere" which means to fragment (Wertenberger).

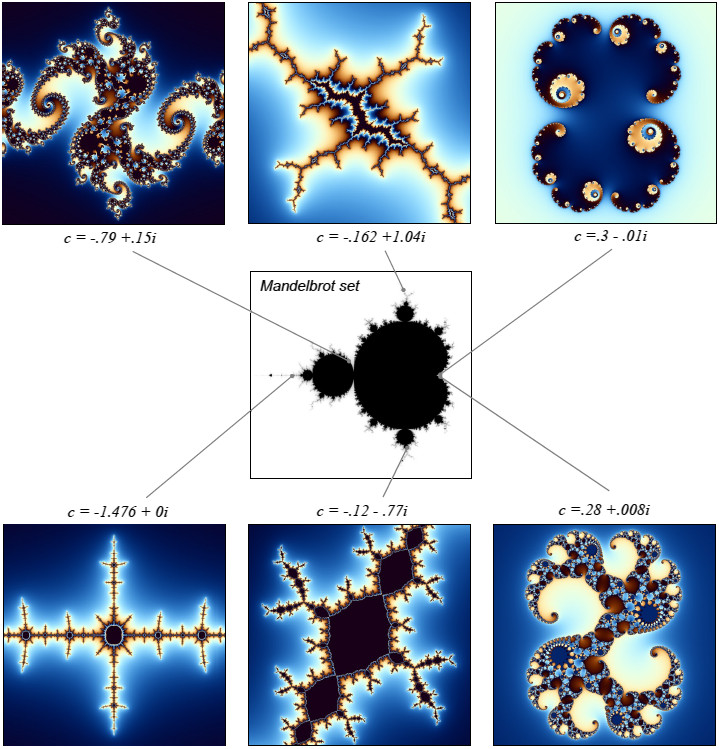
Then in 1980 Mandelbrot created his own version of a function that would combine every single one of the Julia sets into one and the image that resulted is what we call the Mandelbrot set. When you zoom in on different parts of this set, you can see the different Julia sets embedded within the patterns. Unfortunately for a while, Mandelbrot's ideas were not accepted as practical or significant mathematics and considered computerized artwork (Jersey & Schwarz, 2011).

We know that fractals have been implicitly used and unconsciously used for pretty much all of time because we see them all over in nature. But were they consciously known and used before Mandelbrot came along?

It turns out that fractals were used by various indigenous peoples in Africa much before Mandelbrot and Julia's time. All over Africa, Dr. Ron Eglash found that a significant number of villages were based off of fractal patterns. For example, one community had self-similar rectangles and the royal insignia had a rectangle within a rectangle within a rectangle. Did these African tribes actually know the algorithms to their construction and understand the concepts of fractals? Eglash found that some of them just liked the way they looked, but many of them did actually have algorithms for these patterns. Some of the algorithms and concepts the Africans used were the same as what we know to be the Cantor Set, recursive geometry, and Eulerian paths. Also, a certain religion that practiced Sand divination used lines in the sand based on a recursion algorithm very much like the Cantor set. These lines were essentially binary code. This concept managed to travel to Europe where Liebniz was able to study it and create the binary code applicable in formal mathematics. So just think of it, binary systems originated in Africa (Eglash, 1999)!

Back

link to top