Explanation of Mathematics

Before we dive into the mathematics behind Pascal’s Triangle and the many patterns that have been discovered over time, enjoy this brief video that introduces several of those patterns and their significance.

Now we will provide a brief explanation of the patterns found in Pascal’s Triangle.

Powers of Two:
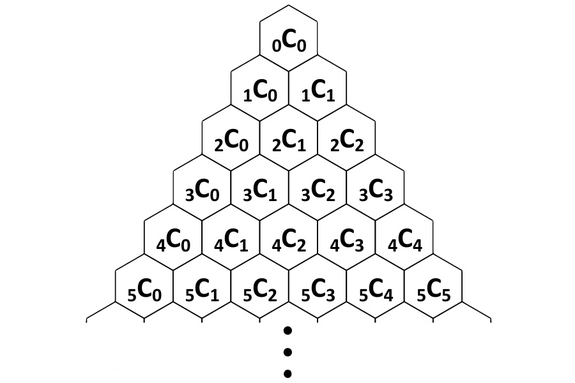
The sum of a horizontal row is always a power of 2.

Magic Elevens:
The numbers within the first 5 rows represent the power of 11.

Triangular & Square Numbers:
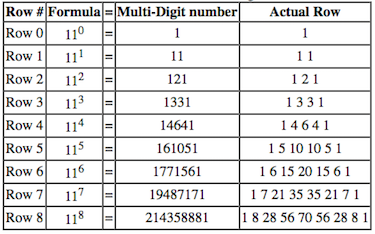
Any two adjacent numbers in the diagonal with triangular numbers will result in a sum, which is a perfect square.

Prime Numbers:
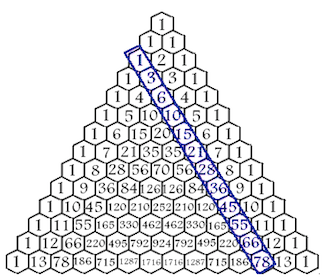
Whenever the second number in a row is prime, the remaining numbers on that same row will be divisible by that prime number.

Hockey Stick Pattern

Catalan Numbers:
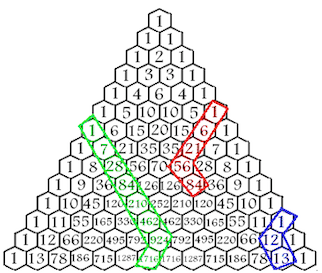
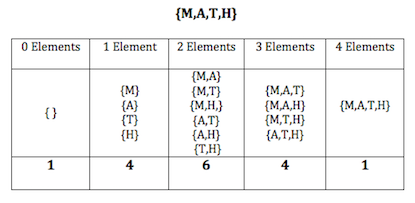
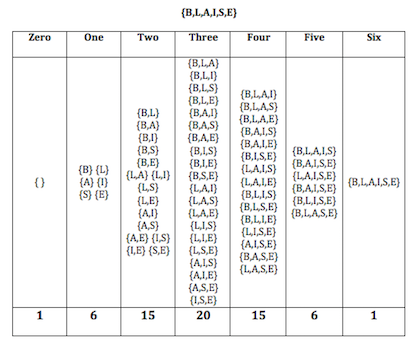
By taking any polygon and calculating the number of ways it can form triangles, one can find a catalan number. In the image below, catalan numbers can be seen within Pascal’s Triangle when the difference of the two numbers highlighted is found.

Fibonacci's Sequence

Fractals:
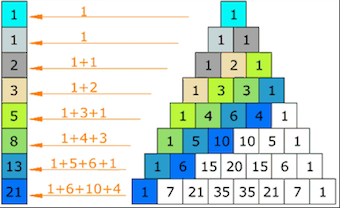
When all the even numbers are shaded one color and the odd numbers another color, another pattern becomes visible. As shown, Pascal’s Triangle has now become the recursive of the famous Sierpinski's Triangle.

Inscribed Polygons:
With each additional vertex placed on the circle, we can find the following line of Pascal’s Triangle based on the number of each polygon made from those points on the circle. This is depicted in the picture below and can also be discovered using the applet here.

Polygonal Numbers:
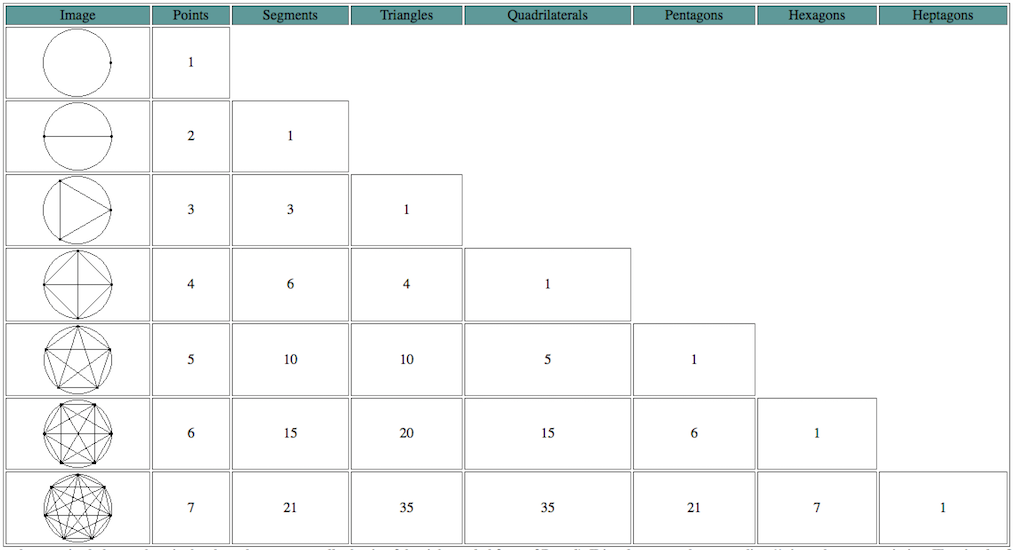
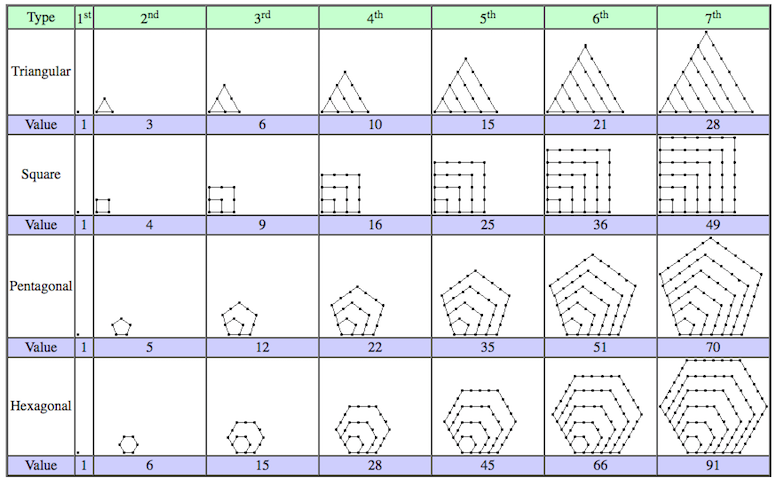
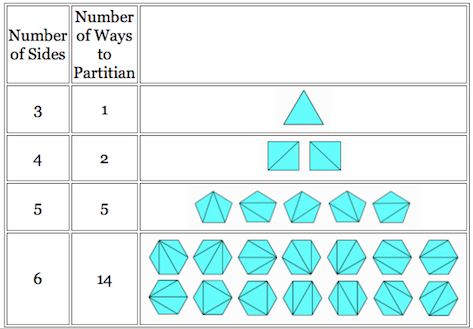
Another pattern that exists within Pascal’s Triangle shows the total number of vertices when different polygons are formed. We can see examples of this in the image below. Now the numbers for each type may not seem immediately connected to Pascal’s Triangle when given a first glance. However, they are found through simple application of Pascal’s Triangle. We will now explain. Note that the triangular numbers exist in the third diagonal as mentioned earlier. The remaining polygonal numbers are not readily visible. The total number of vertices must be found for each additional larger polygon which is formed using the existing polygons already in place. The Shi-Cheng formula was derived in order for one to quickly solve for the total number of vertices where x refers to the type of polygon and n refers to the number of polygons. Let us consider the case where we want to find the total number of vertices for a Hexagon in the 7th stage as shown in the image. We would let x=6 and n=7. Because x is even in this case, we would use the Shi-Cheng Formula as follows. We solve for y by using y=x/2-1. Then we can use the formula n+y(n^2-n) to solve. Therefore, in our case, y=6/2 - 1, which equals 2. Following this, we would get 7+2(49-7), which equals 91. Note that in the case where x is odd, then we would use y=(x-1)/2 and then the formula (-(n^2)+3n+2n^2y-2ny)/2.
Now perhaps one would like a simpler method. There is such a method, and it includes the use of Pascal’s Triangle. Furthermore, it uses what is called the Winton Formula, which applies the 2nd and 3rd diagonal in Pascal’s Triangle. We will use the same example where we are solving for the nth x-gonal number, and n=7 and x=6. The Winton formula finds the nth row in Pascal’s Triangle, finds the number in the third diagonal (triangular numbers), then multiplies that number by (x-2). Following this, the resulting product is then added to the number from the 2nd diagonal, still in the same nth row. This formula can be written as ((n^2-n)/2) x (x-2) + n. In our example where n=7 and x=6, this would look like ((49-7)/2) x (6-2) + 7 = 21(triangular number on 7th row) x 4 + 7(Number in second diagonal on 7th row) = 91. Either formula works, but the Winton Formula may be preferred so one may be more efficient by using Pascal’s Triangle. Regardless, the Shi-Cheng formula or the Winton formula will both give the correct result, which may be quickly tested using the applet found under Polygonal Numbers on this link.

We have observed that Pascal’s triangle contains many mathematical patterns. Something else to be considered about Pascal’s triangle is how subsets are closely related to it. We may consider the following examples: First, we can find all of the subsets for the letters in the word MATH by separating them according to the number of elements. We can then do the same for the name BLAISE. The subsets of each can be seen in the tables below.

Are we beginning to observe a pattern? By the given examples, we have discovered the connection between Pascal’s triangle and subsets. In fact, what we really have discovered is the connection between Pascal’s triangle and the number of possible combinations, as that is what the number of subsets represents. The following is an image of Pascal’s triangle represented with combination notation.

Now the initial pattern we notice in Pascal’s triangle is how a number on any given row is the sum of the two numbers above it. Considering the triangle with combination notation, we can again observe this pattern. If studying algebra, one will learn that the numbers within Pascal’s Triangle correspond with the coefficients in a binomial expansion. This leads us to ask the question of why exactly the coefficients in binomial expansions are actually combinations? We may consider the general case of (x+y)^n. Note that order does not matter, which means we will be working with combinations. We will be thinking about choosing an x to find each coefficient. Starting with the first term when (x+y)^n is expanded, we know it will contain only x’s and no y’s with a coefficient of 1. Since there is only one way to choose zero y’s from n, then this is represented as C(n,0) = 1. Next will be the y term. There are n ways to choose one y from n possibilities. Just as the coefficient of y is n, similarly C(n,1) = n. Following this is the y^2 term. There are n ways for the first y, then (n-1) ways for the second y. This means there would be (n(n-1))/2! Possible ways of choosing two y’s which would be the coefficient for y^2. In other words, C(n,2) = (n(n-1))/2!. Continuing this process we would discover that C(n,3) = n(n-1)(n-2)/3!. Furthermore, the term y^r would have the coefficient C(n,r) = n(n-1)(n-2)(n-3)…(n-r+1)/r!. Now test it out on Pascal’s Triangle. For any case it will be proven true. In order to see a more specific example, observe the following binomial expansion. (x + y)^4 = _______(x^4) + _____(x^3)(y) + _____(x^2)(y^2) + _____ (x)(y^3) + _____(y^4) (x + y)^4 = C(4,0)*(x^4) + C(4,1)*(x^3)(y) + C(4,2)*(x^2)(y^2) + C(4,3)* (x)(y^3) + C(4,4)*(y^4) OR (x + y)^4 = 1(x^4) + 4(x^3)(y) + 6(x^2)(y^2) + 4(x)(y^3) + 1(y^4) Now we can clearly see how the coefficients can be directly found in Pascal’s Triangle.