Old Number Systems from Around the World

Babylonians

In math and counting today, we use a decimal system (base 10). This means essentially that our numbers repeat themselves after every ten units, value increasing as the units change position. For example, we can count using numbers 0-9, then the next number is ten, and we have a one in the “tens” unit place, and are back to zero in the units position. The early Babylonians and Sumerians ,however, used a sexigesimal system or in other words: base 60, so their numbers repeated and changed position after every 60 units (Seife, 5-23).

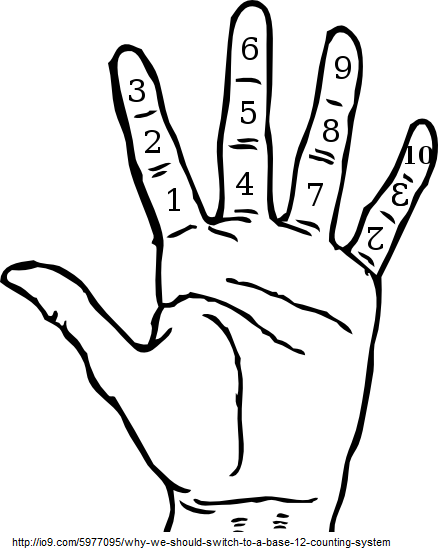
It remains a mystery why they chose such a large base. Some speculations are that it is because it is a relatively low number with a large number of divisors, and it has all of the first six integers as factors. Possibly it is the result of mixing base 5 and base 12, both of which can be done on fingers (Seife, 5-23).

One large contribution that we need to thank the Babylonians for is a positional numbering system. From the studies that have been conducted, it is clear that the Babylonians were the only pre-Grecian people who made use of a positional number system. A positional number system, like what we currently use, is superior to others because you only have to have a few different symbols to express an infinite number of numbers. In a positional number system, the position of the number, with relation to the other numbers, is what determines its worth.(Burton, 23-27).
For example, our number " 12 ". The symbols that make up this quantity are "1" and "2". In a non-positional number system, we would merely have an expression of the number "3", yet we understand that the "1" is in the "tens place" and thus represents that quantity, while the "2" is in the "ones place" so represents two of units of the quantity 1. Thus "12"= "10+2."
No one, at this time in history, had accepted the number "zero" yet. So one problem with this positional numbering system was how do you tell apart numbers such as 10001 and 101? Though the Babylonians did not accept zero as a number, the way we accept it now, they accepted its existence as a place-holder, which was a significant step in the right direction.
Back to Top

The Mayans:

The Mayan Number System used a vesigesimal number system, which works with a base of 20. It is thought that this may be because it was so hot, there was no need to wear shoes, so their toes were just as readily available as their fingers, for counting purposes. This number systems dates back to the 4th century, and was approximately 1,000 years more advanced than the Europeans at the time. They used a dot to represent the quantity one and a dash to represent a quantity of five (Burton, 7-8).

The Mayans were, as we believe, the first to symbolize the idea of zero, or " nothing ". It is also from them that we get our calendar year. They used a base of 18 for this, and each month contained 20 days, then the five days at the end of the year were added on (Ifrah, 9,36).

Mayan counting applet.
Back to Top

Incas

A South American Indian tribe, or collection of tribes, known as the Incas used knotted chords as number strings. When the Spanish Conquistadors arived, they noted that each city in Peru had an “official of the knots” who maintained accounts, using these knotted chords, or “Quipus”. They had three different types of knots, a figure 8 knot to represent 1, a long knot representing values between 2 and 9, depending on the number of twists in the knot, and a single knot which also represented 1. The first two knots appeared on the lower valued chords, while the single knot appeared on the higher valued ones. Chords in the bunch that did not have any knots acted as a placeholder, or a form of zero (Burton, 6).
Back to Top