Back in 800 A.D, Arab scholars invented a system that could break Caesar shift ciphers and other monoalphabetic substitution ciphers. The system that the Arab's invented has come to be known as frequency analysis, (a branch of cryptanalysis), which is the science of unscrambling a message without knowledge of the key.
Arabian theologians studied the revelations of Muhammad. There was much speculation as to what revelations and documents came from Muhammad and what documents and revelations did not. This was done by studying the etymology of words and the structure of sentences, to test whether particular texts were consistent with the linguistic patterns of the Prophet. They also analyzed individual letters, and in particular they discovered that some letters are more common than others (Singh 1999).
The Arabs used this knowledge that some letters were more common than others to crack codes. The earliest known description of the technique is by the ninth-century scientist al-Kindl. al-Kindl authored what is known as A Manuscript on Deciphering Cryptographic Messages. To explain how frequency analysis worked, he wrote the following:
"One way to solve an encrypted message, if we know its language, is to find a different plaintext of the same language long enough to fill one sheet or so, and then we count the occurrences of each letter. We call the most frequently occurring letter the "first," the next most occurring letter the "second," the following most occurring letter the "third," and so on, until we account for all the different letters in the plaintext sample. Then we look at the ciphertext we want to solve and we also classify its symbols. We find the most occurring symbol and change it to the form of the "first" letter of the plaintext sample, the next most common symbol is changed to the form of the "second" letter, and the third most common symbol is changed to the form of the "third" letter, and so on, until we account for all symbols of the cryptogram we want to solve."
It may be helpful to give an example of what al-Kindl mentioned with the English alphabet. In the book Cipher Systems: The Protection of Communication, written by Henry Beker, a study was done in which passages were taken from English newspapers and various novels and were analyzed. 100,362 alphabet characters were counted and the following table was created about how frequently each letter is used: (not surprisingly, letter frequencies are roughly the same today)
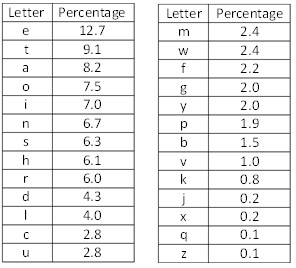
E is the most commonly used letter, followed by T, followed by A, etc. So, if I come across the following message: "TLLA HA LPNOA" my first step would be to count up how many times each letter is used.
T = 1, L = 3, A = 3, H = 1, P = 1, N = 1, O = 1. I will then guess that L in the ciphertext represents E or T in the plaintext and A in the ciphertext represents either T or E in the plaintext. Because I see a double L near the beginning of the message, I will guess that L in the ciphertext represent E in the plaintext and that A in the ciphertext represents T in the plaintext. Substituting letters, I obtain the following the message: "xEET xT ExxxT."
Now looking back at the ciphertext, a sensible guess would be T in the ciphertext represents M in the plaintext (making the first word "meet") and I will guess that H in the ciphertext represents A (making the second word "at"). I can now build the following table:

I now note that to go from the 8th letter H to the 1st letter A, I subtract 7. To go from the 12th letter L to the 5th letter E, I subtract 7. I can now guess that whoever wrote the message used a Caesar shift cipher with key = 7. I would then finish filling in my table. I can then figure out that P in the ciphertext represents I in the plaintext, N in the ciphertext represents G in the plaintext, and O in the ciphertext represents H in the plaintext. I now have obtained the plaintext message "Meet at eight."