The Pythagorean Theorem


The Pythagorean Theorem is , “the one theorem that just about every student remembers learning in school; it’s the theorem about the side lengths of a right angled triangle which Euclid attributed to Pythagoras when writing Proposition 47 of The Elements” (Percy&Carr, 8). Similarly to Euclid’s misleading nickname of “Father of Geometry,” Pythagoras and the Pythagoreans are mistakenly credited for ‘discovering’ the Pythagorean theorem. It’s important to keep in mind that the Greeks were recognized for being the first to use deductive reasoning and that their purpose for engaging in mathematics was not for necessity of the application in everyday life, instead for the sake of mathematics. The purpose of application was that of the Egyptians and the Babylonians. The Egyptians had been aware of Pythagorean triples, but it was the Babylonians who made use of the Pythagorean Theorem, “Although tradition is unanimous in ascribing the so-called Pythagorean theorem to the great teacher himself,we have seen that the Babylonians knew the result for certain specific triangles at least a millennium earlier” (Burton 107). Therefore, it was the Greeks, along with several other mathematicians and even a president of the United States, that took the time to prove the theorem.

Here are some examples of the proofs of the Pythagorean theorem:

Theorem: The square on the hypotenuse of a right triangle is equal to the sum of the squares on the two legs.


Pythagoras’ Proof


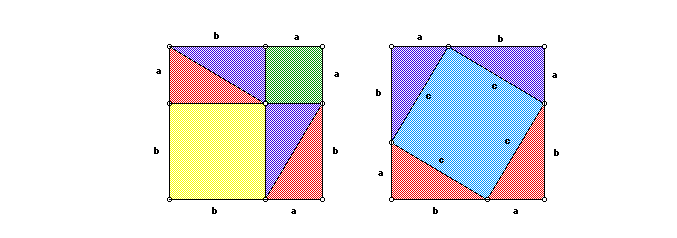
Let a, b, c denote the legs and the hypotenuse of the given right triangle, and consider the two squares in the given right triangle, and consider the two squares in the accompanying figure, each having a+b as its side. The first square is dissected into six pieces-namely, the two squares on the legs and four right triangles congruent to the given triangle. The second square is dissected into five pieces-namely, the square on the hypotenuse and four right triangles congruent to the given triangle. By subtracting equals from equals, it now follows that the square on the hypotenuse is equal to the sum of the squares on the legs.


The area of the first square is given by: (a+b)2 or 4(½ab)2 + a2 + b2
The area of the second square is given by: (a+b)2 or 4(½ab)2 + a2 + b2
Since the squares have equal areas, we can set them equal to another and subtract like terms:
4(½ab)2 + a2 + b2 = 4(½ab)+ c2
After we combine like terms, we end with: a2 + b2 = c2
This concludes Pythagoras’ proof.


Bhaskara’s Proof


Bhaskara’s proof is also a dissection proof. It is similar to the proof provided by Pythagoras. Bhaskar was born in India and was one of the most important Hindu mathematicians of the second century. He used the following diagrams in proving the Pythagorean Theorem:


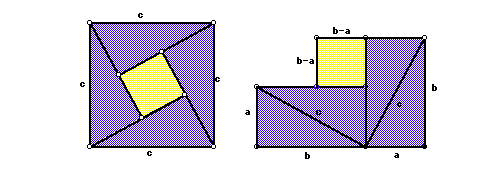
In the above diagrams, the blue triangles are all congruent and the yellow squares are congruent. First, we need to find the area of the big square in two different ways. Let’s find the area using the area formula for a square.
Area of big square: A= c2
Now we find the are of each of the components and then sum the areas.
Area of blue triangles: 4(½)ab
Area of yellow square: (b-a)2
Area of the big square:
= 4(½)ab + (b-a)2
= 2ab+b2-2ab+ a2
= b2 + a2
Therefore, the square has the same area no matter how you find it:
A= a2 + b2 = c2
This concludes Bhaskara’s proof.


President James Garfield’s Proof


The twentieth president of the United States of America gave the following proof to the Pythagorean Theorem. He discovered this proof five years before he became President. He hit upon this proof during a mathematics discussion with some Congress members, and it was later published in the New England Journal of Education. The proof depends on calculating the area of a right trapezoid two different ways. The first way is by using the area formula of a trapezoid and the second is by summing the areas of the three right triangles that can be constructed in the trapezoid. He used the following trapezoid in developing his proof.


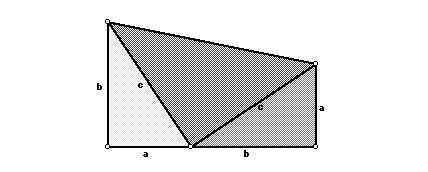
First, we need to find the area of the trapezoid by using the area formula of the trapezoid.
A= (½) h( b1 +b2 )

In the above diagram, h= a+ b; b1= a and b2=b.
A= (½)(a+b)(a+b)
= (½) (a2 + 2ab + b2).
Now, let’s find the area of the trapezoid by summing the area of the three right triangles.
The area of the yellow triangle is: A=½(ba).
The area of the red triangle is: A=½(c2)
The area of the blue triangle is: A=½(ab).
The sum of the area of the triangles is: ½(ba)+½(c2) + ½(ab)
= ½(ba + c2 +ab)
= ½( 2ab+ c2).
Because this area is equal to the area of the trapezoid, we have the following relation:
(½)(a2+2ab+b2)=(½)(2ab+c2)
Multiplying both sides by 2 and subtracting 2ab from both sides, we get:
a2 + b2 = c2
This concludes Garfield’s proof.

(Head,A).


Another Proof...

Here's an Geogebra applet that demonstrates another proof of the Pythagorean Theorem:

If you move the vertices of the triangle in the center, you'll notice that the side lenghts change, but the Pythagorean Theorem holds true.

(Head,A).