
The Child Prodigy
It is said that as a school boy (around age 7) his teacher set his class a task meant to keep them quiet; summing all numbers from one to one hundred. Gauss, the prodigy, very quickly deduced the answer to be 5050 and turned it in on his slate. Instead of working on the addition of one hundred numbers Gauss saw a way of performing the computation generally. He noted that 1+100=101 and so did 99+2 and so did 98+3 and so on throughout totaling 100 pairs which sum to 101. Multiplying this out we have 100*101=10100, but we counted the number of necessary pairs twice and so we divide our number by 2 yielding 10100/2=5050. The general pattern for deducing the sum of the first n number by n(n+1)/2. Remember, he did this at or around age 7 which demonstrates his exceptional computational skills but additionally, his ability to recognize underlying patterns and develop useful conjectures. A nice visual way of seeing this computation is featured here.
Monument to Gauss
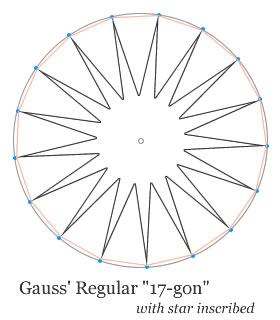
The constructibility of objects using a straight edge and compass was a concept dating back to the days of Euclid. For an overview
of how this works click here. At the time when Gauss was living on the earth, the list of constructible regular n-gons (each side of
a n-sided polygon has equal length and interior angles equal) was thought to be complete and did not include a 17-sided regular
polygon. Gauss proved that the list was not complete and showed other n-gons to be possible extending the list. A brief video
showing the construction of a heptadecagon can be seen here .
He was so proud of this feat that he wanted it to be carved into his
gravestone, but as it looked so much like a circle the request was denied. It was however inscribed on a monument that stands in his
birthplace of Brunswick.


Number Theory
It is not my purpose to get too much into the number theory overly, but attributed to Gauss are many theorems concerning number theory including the proof of Quadratic reciprocity , modular arithmetic, and his prime number theorem.
Gaussian ( normal ) Distribution
The central limit theorem states that independent, identically distributed samples from a population will follow the normal distribution and will therefore approximate the population mean and variance. Gauss applied the normal distribution with regards to approximating the orbits of planets. The observations, he reasoned, come from a normal distribution as they are prone to errors in measurement. Using the properties of normal distributions and his method of least squares, he was able to determine the orbit of the planetoid Ceres after it had been lost in the glare of the sun. It was found in December of that year about where he predicted. The normal distribution is a continuous probability density function from which the probabilities of certain values can be computed.
Method of Least Squares
This method is used to determine a line of best fit for two variables or more. The simple case is that of bivariate and we are trying
to determine how one variable affects the other. The difference between the line and the observed point is the residual
or the error
and has a normal distribution. This error is minimized by finding the partial derivative of the sum of squares of the difference
between our yet unknown line (represented by y hat) divided by the standard error and then setting the derivative to 0 and solving
for the predictive y-hat.
Try to see if you can eyeball
the best fit line. Check the box to find the calculated best fit line.