Zero-moving through time, from nonexistence, to existence, and some of the steps along the way
Numbers have not always existed, even more so than just numbers as we know them. In a world without language at all. A long, long time ago, only the most basic idea of zero existed. The cave man probably realized that they didn't have any food. Your dog even realizes that. From there, a deeper understanding of the "idea of zero" took place as the cave man surely found some way, a gesture maybe, to show that they had nothing. This is still a long ways away from the number zero, or even any other number. At this point (A point in time with no real date,) the cave men could probably only understand that they had nothing, or that they had something. I must mention here that there is simply no evidence to support anything more than this, looking this far back in time. However, observations of different cultures suggest that the cave men likely quickly developed some system to keep track of quantity. Most likely a notch on a piece of wood, or a pile of rocks. Still no actual numbers, just unit measurements of different sorts; this was the beginning of numbers. (Burton, 2006)
As far as 30,000 B.C. there is evidence of moving past just using unit measurements. In 1937 a young wolf bone was discovered in Czechoslovakia with 55 engraved notches organized into groups of fives. (Burton, 2006) Now instead of just recognizing unit measurements, groups of five were being recognized. It's worth mentioning that this grouping of the arbitrary number five, seems to stem from the fact that we have five fingers on each hand. Here it is easy to see why there would be no consideration of zero. In simple daily life, there isn't really any need for zero.
Going through the entire development of the number system would be very extensive and exhaustive. It is important to understand a brief interpretation of the development of numbers to be able to see why zero wasn't invented/discovered earlier on, and then to see why the world found it so hard, or unnecessary to accept for a very long time.
Zero as a place holder
The Sumerians, made a huge step towards zero being recognized as a place holder but, I'll get to that later. For now, It is important to recognize that the Sumerians developed a decimal based numerical system, and also that they recognized the benefit of using a base 60 numerical system. They first used a reed to impress a circle or a half circle in clay to write their numbers but they eventually used a three sided stylus that could be used to make these markings: 
(one) or, when turned differently, 
(Ten.) The first used in the units place, and the second was in the 10's place. To illustrate this, observe how 
represents 30. All this happened around 3000-2500 B.C., in what we now recognize as Iraq. (Kaplan, 1999)
The Sumerians succumbed to the Akkadians around 2500 B.C. and then by 2000 B.C. the group became known as the Babylonians (Old Babylonians to us.) By then they still had no symbol for 5 but did have a symbol for 60 to use with their 60 base system. It is unclear how early the symbol was used, or if the Akkadians used it. The symbol was
. You might be confused because isn't that the symbol for the unit/one. You are not the only ones who were confused, and this is actually what led to the Idea of a place holder, (not using the number zero as a place holder though.) Consider the number 65, which the Babylonians wrote as
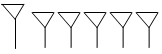. It already seems reasonably confusing to know what number is meant. Now compare the numbers 120 and 2 in Babylonian, 
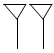(120), 
. (2). It is extremely hard to know what number is meant. Try considering the difference of 7,205 and 125. For the number 65 they might have tried leaving spaces to show the difference of the decimal places, but a space can be somewhat arbitrary and confusion still remained. Also, Spaces don't help when comparing the numbers 120 and 2. This is where the pace holder was finally recognized.
Some Babylonian between the third and sixth century B.C., constructed the sign 
to be used to signify a place holder (Kaplan, 1999). Kaplan commented on this historic innovation:
Whoever it was, in the latter days of Babylon, that first gave to airy nothing a local habitation and a name, has left none himself. Perhaps that double wedge fittingly commemorates his place in history. (Kaplan, 1999)
It was here that a place holder was discovered, but also a symbol for nothing. It is very important to recognize here though, that does not represent a number, but nothing, or a blank. Burton seems to agree with this as he explains that this, "divider," was used from 300 B.C. on (Burton, 2006)
Turn your attention to the Egyptian civilization which had sprouted itself along the Nile River. They are known to be one of the earliest civilizations to explore mathematics, but not really for mathematics sake, but for the geometry they needed to use. This need for geometry pushed them forward in mathematics but created a boundary in which zero was not included. In The Biography of a Dangerous Idea, Seife explains how the flooding Nile was responsible for their need of geometry. Each year the Nile flooded, the rich farmland they depended on was covered with water and dirt, destroying their property markers. After each flood, they needed a way to re-construct the property boundaries. "Rope stretchers" would go and measure out each of the boundaries. Geometry was the tool they used to accomplish this, but that tool requires numbers. (Seif, 2000)
"As early as 3500 B.C., the Egyptians had a fully developed number system that would allow counting to continue indefinitely," as long as they kept on adding new symbols anyways. The Book of the Dead, possibly from the First Dynasty, provides a recording of this number system. In it you see that there is a unique symbol for the unit 1, for 10, 100, 1000, 10000, and so on. You might want to compare this to the timeline of the Babylonians and their innovations. (Burton, 2006)
The Egyptians lived approximately at the same time but they do not have any need for place holders in their numeric system. Even without place holders, they managed to develop a deep understanding of geometric math. Besides not needing place holders for this, they also never needed to consider zero for any use in geometry was not apparent to them. The Egyptians never seemed to do math, for math sake, and perhaps this is why their great mathematical enlightenment so quickly ran into walls.
Moving from around 3500B.c., to the 5th century B.C., the Greek civilization was also tied to geometry, but began looking at it for math sake. They quickly took what they learned from the Egyptians and pressed forward into the number system and mathematics. However, they clung onto their own system of numbers instead of using the Babylonian system that took advantage of decimal places and place holders that would have made dealing with fractions much easier. They considered numbers and philosophy inseparable, and looked at both of them very seriously. Perhaps too seriously when you consider what happened to Hippasus of Metapontum, which I will get to later. (Seife, pp. 26)
The Greek alphabetic numeral system, developed in the 5th century B.C., was much more extensive than the Egyptians. They had different, alphabetic, symbols for the numbers 1 through 10, and then for each of the Tens up to 100 and each of the 100's up to 900. Thus they could count up to 999 with these symbols by placing them in order from highest to lowest, left to right. They could represent larger numbers though. By placing an accent mark before a number, it would indicate that that number is to be multiplied by 1000. They also introduced the myriad which could be placed next to a number to indicate that it is to be multiplied by 10000, including itself. Also, to indicate that a letter is to mean a number, they would put a bar over the letter or letters. In 150 A.D. an Alexandrian, Ptolemy, used the omicron, which is the first letter of the Greek word ovδεv, meaning "nothing," to better meet the needs of doing his calculations for his work in astronomy (Burton, 2006).Many Greek astronomers by his time would use a Babylonian decimal system with place holders, but would convert their results back into their number system. However, there is still no indication that he considered it as the number zero, he just used it as a place holder.
By now we have seen how difficult and diverse the construction on numeric systems were even though there are many numeric systems that have not been mentioned. The Roman numeral system you probably are familiar with; can you think of the Roman numeral for zero? Many Cultures have come incredibly close to discovering the number zero, but none have done so yet. Even in the period from 350 to 200 B.C., with Euclid and his 5 elements, and Archimedes, the number zero was ignored and pushed aside, for the most part anyways.Interestingly enough though, there does seem to be evidence that there was consideration of the idea of the number zero, without realizing what they were doing. Zeno's paradox, around 490 B.C., and Archimedes's use of the infinite sum to calculate the area of a conic section, are excellent examples. I will go into further detail of these in the next section.
Babylonian numbersystem appletZero as Symbol, and a Number
The use of a "place holder" was essentially rediscovered in India soon after Rome fell in 476 A.D. Sometime beginning in the 5th century A.D. The Indian culture moved from the Greek type numeration system to a Babylonian type of numeration system (the ideas likely spread to them as King Alexander the Great penetrated their lands in his conquest, taking parts of those cultures with him.) Note that they used the base 10 system they were familiar with, instead of adopting the base 60 system, but only used 9 numeric symbols. Zero was not used. It is confusing to know when, but at least by the 9th century A.D., the base system of 10, with a zero type "place holder" was definitely in use. It seems as though the Hindu numeral for that place holder closely resembles our number "zero." It is from these Indian/Hindu symbols that our symbols for numbers come from, which is why Seife calls for the recognition that we shouldn't be naming our numerals Arabic numerals. We should recognize them as Indian numerals. (Seif, 2000)
Kaplan has a few intriguing conjectures about how the symbols of place holder began to resemble what we now see as "0." The Greeks used Reckoning boards to tally sums of payment, or dept. In Apulia, the Darius Vase, dating back to the 4th century A.D., was found showing a picture of a Reckoning board; including the signs for monetary values on the board. It includes "o" to indicate one of those values. "o" is Boeotian for obal, a coin worth almost nothing. He suggests that if you didn't have a number for zero, that you might use the closest thing to it, a symbol for almost nothing. He further suggests that this symbol was rediscovered by the Indians in the dust on their counting boards. The Indians dusted their counting boards and used pebbles as counters. Perhaps the sand was used to act as a memory of what calculations had been done. The indentation of the pebble in the sand definitely resembles something familiar, and would also indicate nothing there in return. Kaplan suggests that the Greeks observed this same thing. As we know, Pythagoras and Archimedes loved to do their geometric calculations in the sand. (Kaplan, 1999)
Going back to the Indian culture, we must recognize the importance of the lack of a tie to geometry, like the Greeks and Egyptians had. Since math didn't have to make sense geometrically something new was being considered. For instance, 5-7=-2, or better yet, 5-5=0. This seems to be the first indication that the "place holder zero" was beginning to be recognized as a number itself. It didn't take long however for the Indians to recognize the bizarre nature of zero as a number.